難易度
算数オリンピック 1993年ファイナル
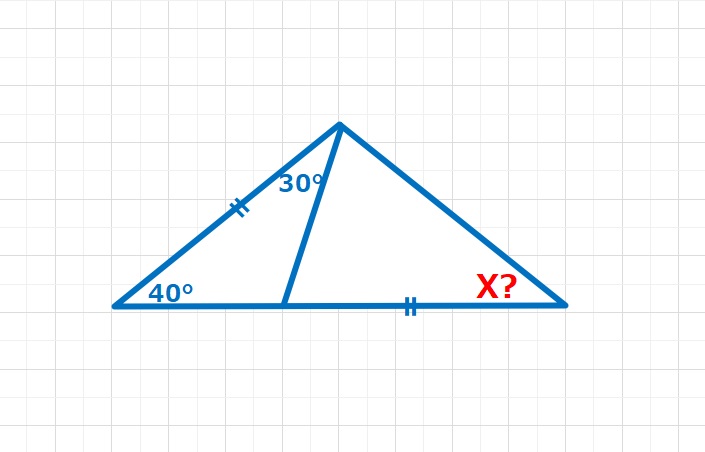
Xは何度ですか?
【ヒント1】
非常にシンプルできれいな形をしてるな、というのが第1印象です。ABとDCの長さが等しく、これをなんとか活用したいです。算数オリンピックでよく使う考え方ですが、△DABをABがDCにかさなるように移動します。移動の仕方は2パターンありますが、下図の移動パターンの方が、きれいな図形ができます。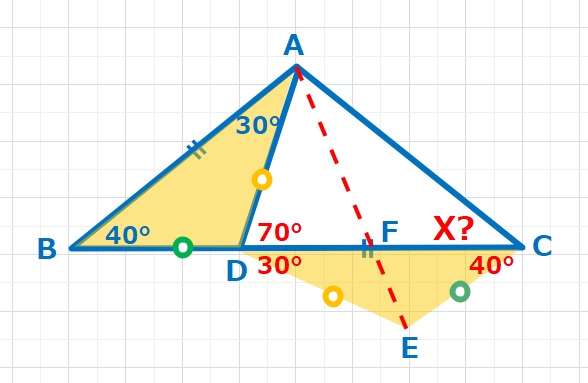
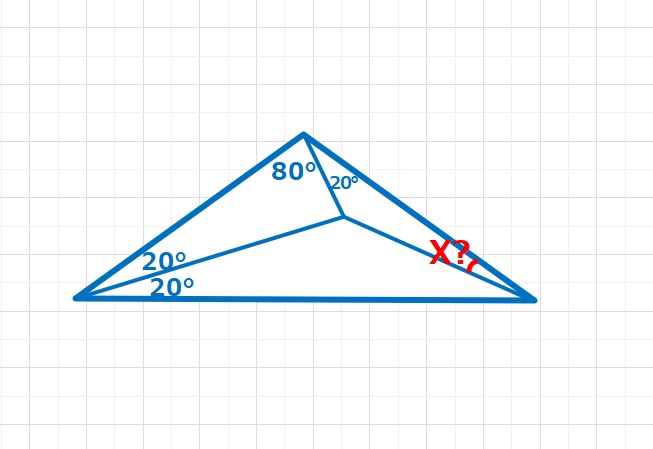
【ヒント2】わかる範囲で角度を書いていくと、二等辺三角形や相似な三角形がたくさん現れてきます。まず△DAEに注目して、DA=DEなので二等辺三角形となり∠DAE=∠DEA=40°。
よって∠AFD=70°となり△ADFはAD=AFの二等辺三角形となります。また△CFEは∠CFE=∠CEF=40°となりますので、CF=CEの二等辺三角形となります。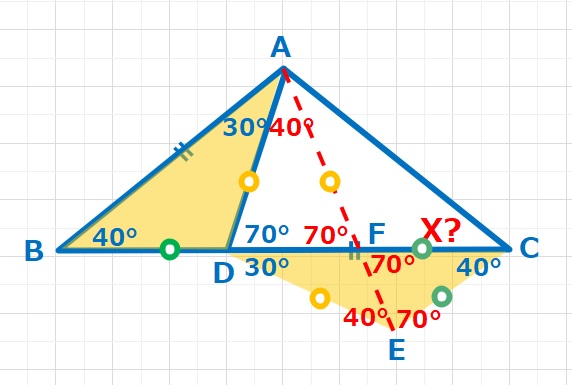
【解答】
△ABFと△ACDにおいて、BD=CFよりBF(BD+DF)=CD(CF+DF),AF=AD,∠AFB=∠ADC=70°なので二辺とその間の角が等しく、合同な三角形となります。よってX=∠ABC=40°・・・(答え)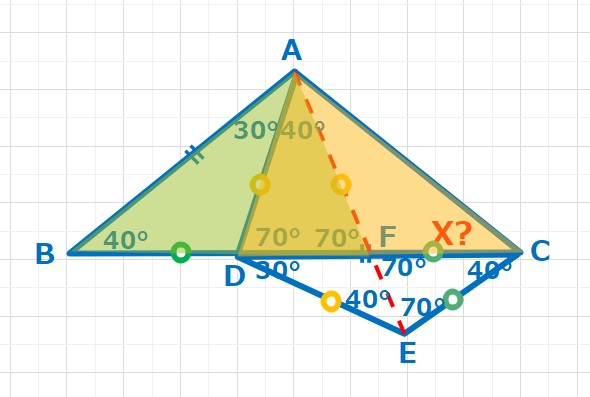
おまけ
AFの補助線が直感的にひくことができれば、二等辺三角形BAFに注目してBA=BF=DCを活用し一瞬で解くことができます。
また、下図のように△ABDを移動した人は、等脚台形ができてX=40°となります。
皆様はどの解答がいちばん美しいと思いますか。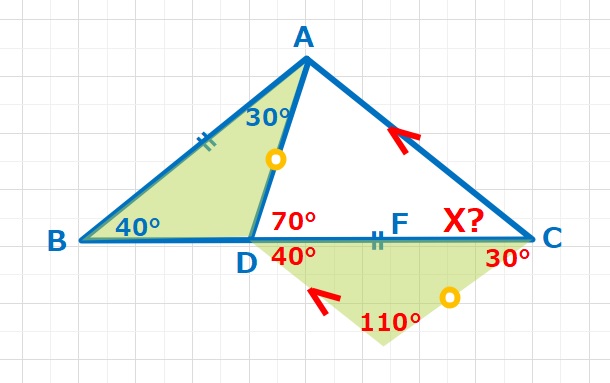
★★★☆☆難関コース 算数オリンピック角度の問題。シンメトリー(対象)な図形をイメージして解く。
 図形
図形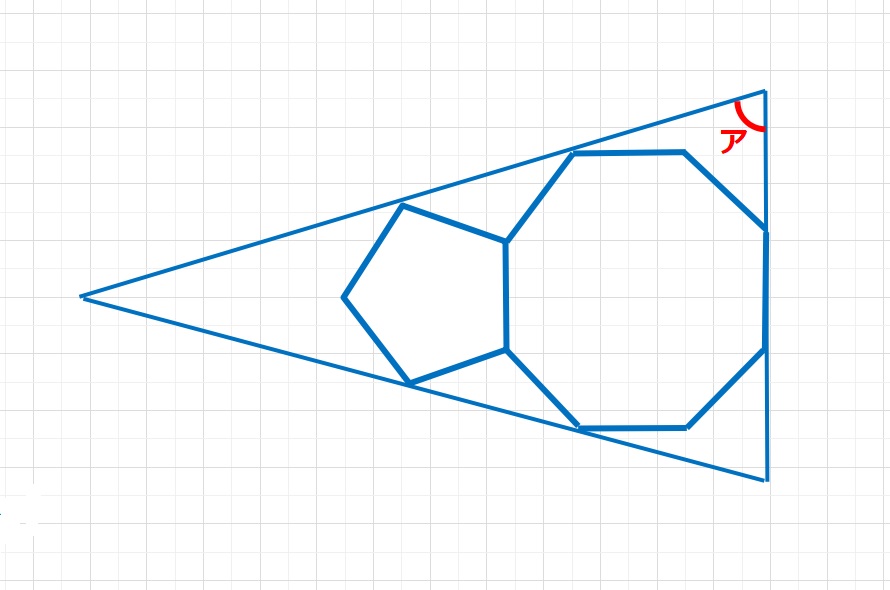
コメント