 数の性質
数の性質 ★★★★★2026!−2025! の末尾に 0 はいくつならぶ?
【問題】2026!−2025! の末尾に 0 はいくつならびますか。ここで 2026!=2026×2025×2024×・・・・×3×2×1、 2025!=2025×2024×2023×・・・・×3×2×1 を表します。...
 数の性質
数の性質 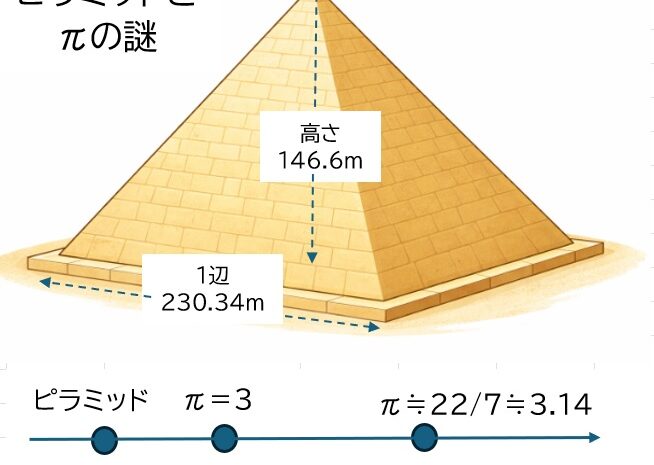 コラム
コラム 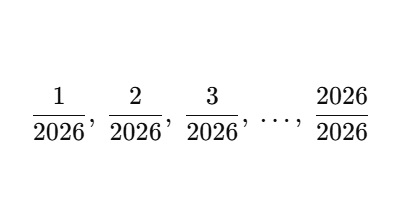 数の性質
数の性質  数の性質
数の性質  コラム
コラム  コラム
コラム 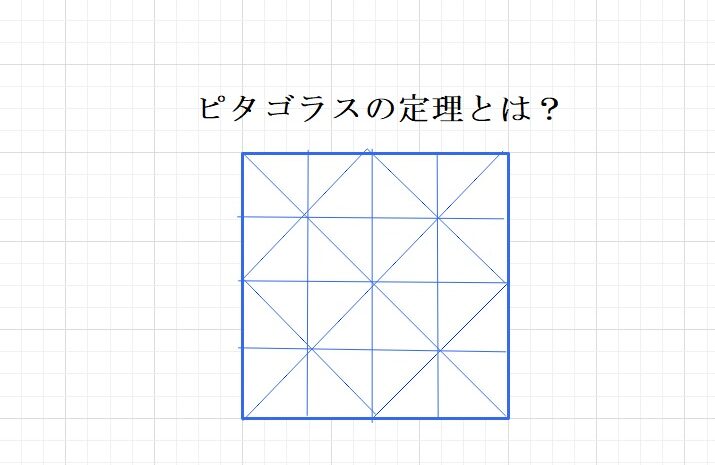 コラム
コラム  コラム
コラム 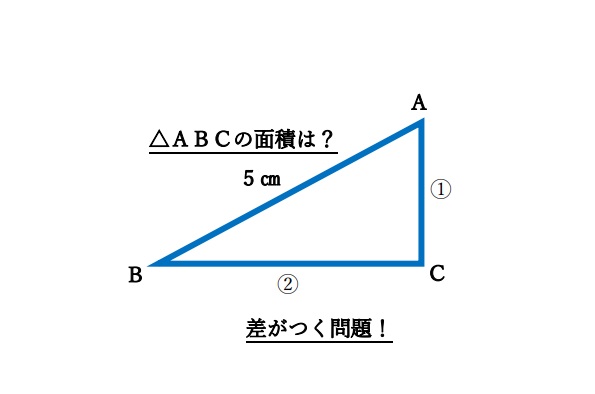 図形問題の武器
図形問題の武器 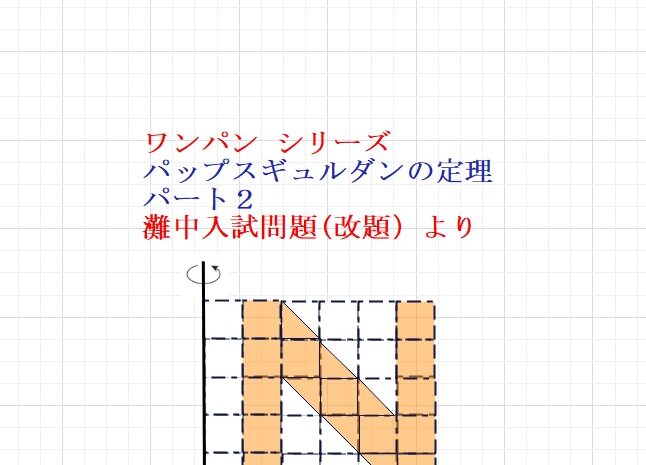 図形問題の武器
図形問題の武器 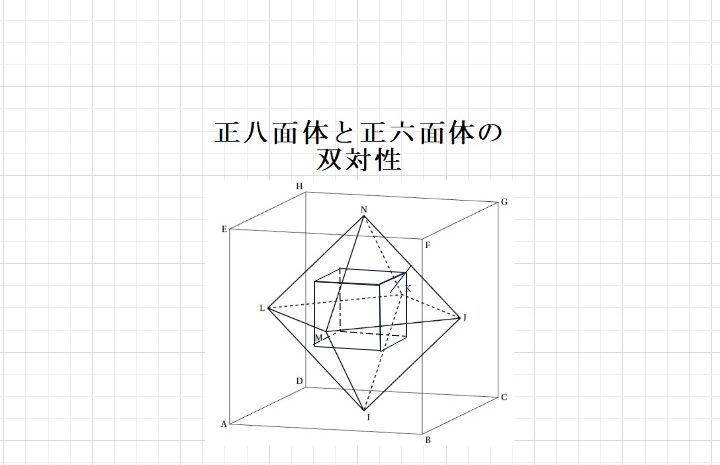 図形問題の武器
図形問題の武器 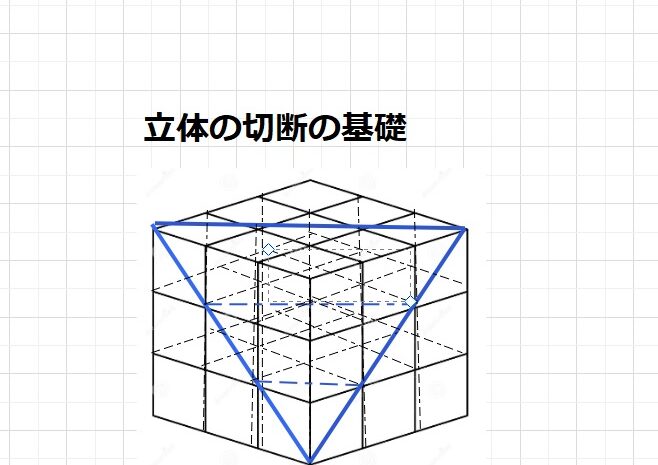 図形問題の武器
図形問題の武器 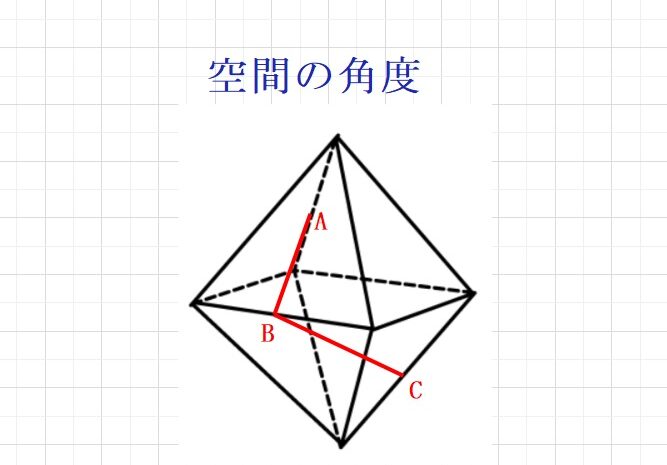 角度の問題
角度の問題 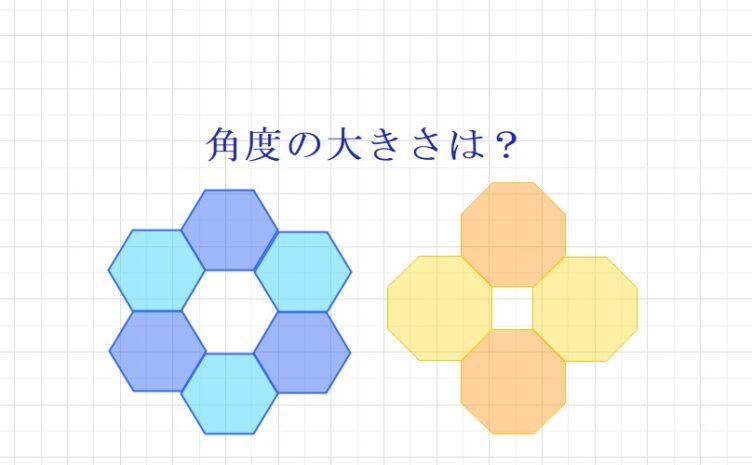 角度の問題
角度の問題 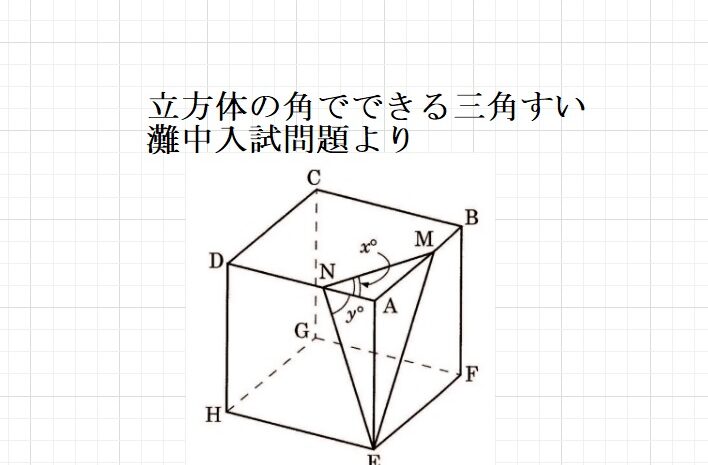 立体の切断
立体の切断 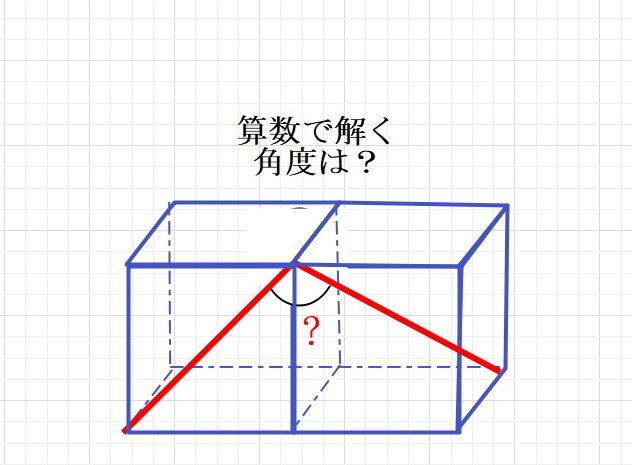 角度の問題
角度の問題 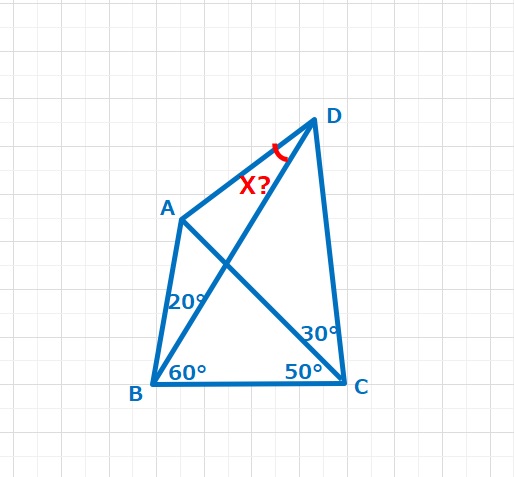 ラングレーの問題
ラングレーの問題 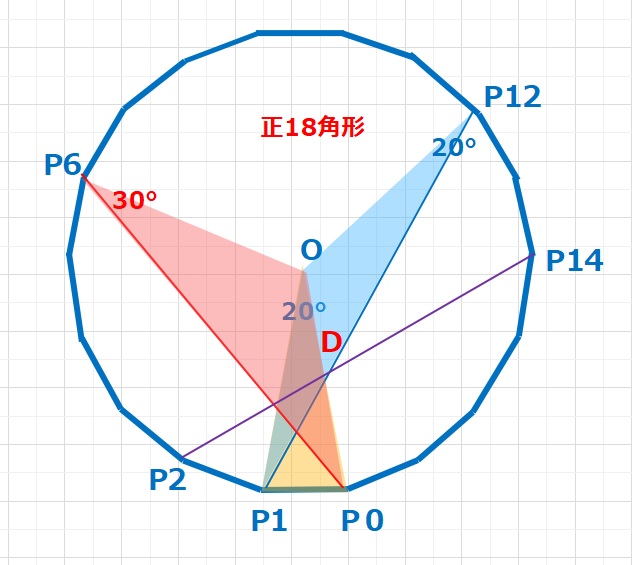 コラム
コラム 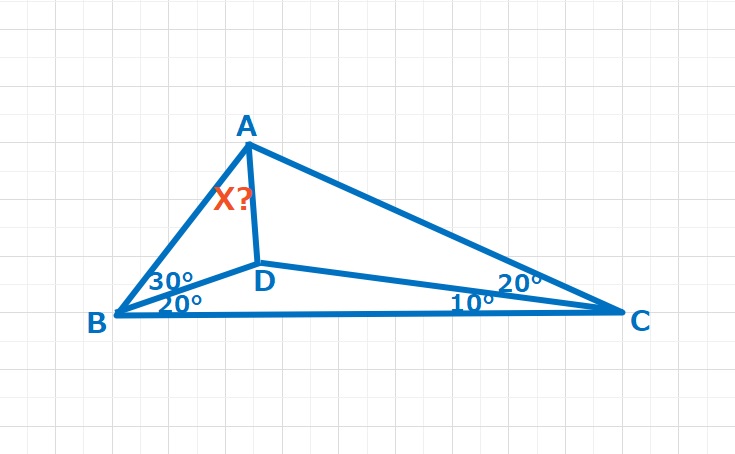 ラングレーの問題
ラングレーの問題 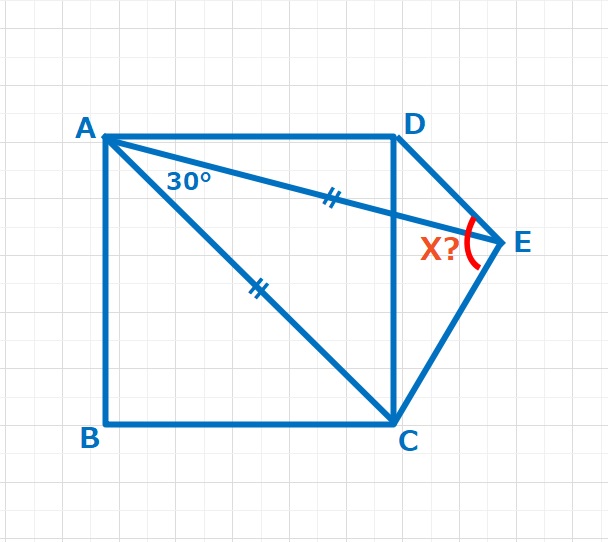 ラングレーの問題
ラングレーの問題