難易度
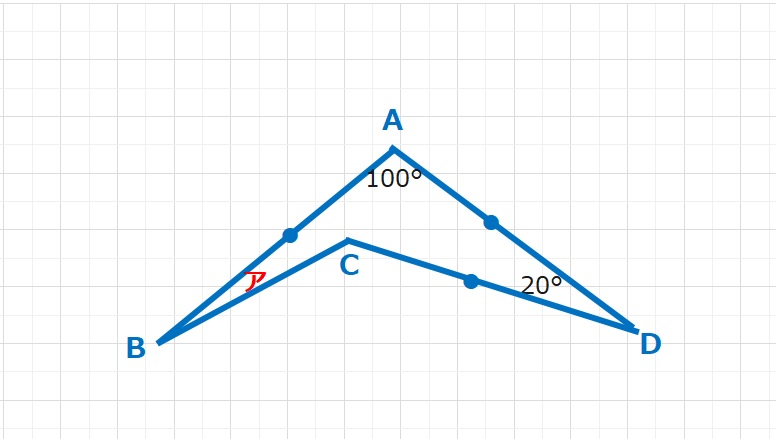
【問題】∠DAB=100°,∠ADC=20°,AB=DC=ADとなる四角形ABCDがあります。ア=∠ABCの角度の大きさは何度ですか。
【ヒント】
すぐに目についたのが、△DACの20,80,80°の二等辺三角形と、△ABDの100,40,40°の二等辺三角形です。△CABとAB=CDに注目して、合同な三角形を、
2角(∠ABC=∠ECD=ア、∠CAB=∠CDE=20°)とその間の辺(AB=CD)が等しくなるように
△EDCをつくりました。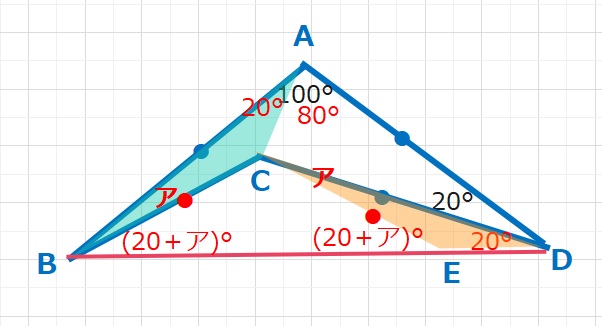
【解答】上の図より、∠ABD=40=20+ア+ア となりますので、
ア+ア=20°となり、ア=10°・・・(答え)
【おまけ】
ADを1辺とする正三角形AEDをつくります。
△ABCと△AECに注目して、2辺(AC共通、AB=AE)とその間の角(∠BAC=∠EAC=20°)が等しいので、合同な三角形となり、ア=∠ABC=∠AECとなります。
緑の線でかこまれた△DCEはDC=DEなので二等辺三角形で、
∠DFC=\(\frac{180-40}{2}\)=70°
ア=∠AFC=∠DFC-∠DFA=70-60=10°・・・(答え)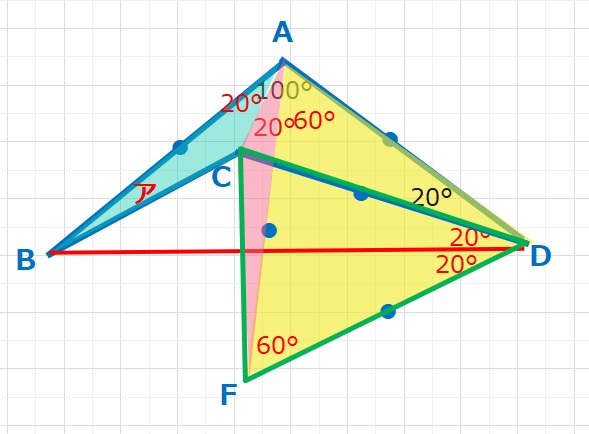
コメント