難易度
【問題】正九角形と図のように2点を共有する正三角形があります。アの角度の大きさは何度ですか。
【ヒント】
正九角形の内角の和は、180×(9-2)=1260°となりますので、1つの内角は
\(\frac{1260}{9}\)=140°です。詳細は図形の武器を参照下さい。
1つ1つ計算していけばよいのですが、7をかけたり9でわったり少し面倒なので
私は、下の図をイメージして計算しています。
正多角形は図のように同じ形の二等辺三角形にわけることができ、正九角形の場合は、
9個の二等辺三角形にわけることができます。
図の対象正より、●の角度の大きさはすべて同じ大きさになり、正多角形の1つの内角は
●2つ分となります。また9等分した1つの二等辺三角形の頂点の角度の大きさは360°を
9等分した大きさになりますので、40°です。
黄緑の二等辺三角形に注目すると、三角形の内角の和は180°なので●2つの角度の大きさは
180-40=140°となります。説明で書くと、長くなりますが、理解すると少しだけ計算が
楽になります。もちろん、●は70°ですね。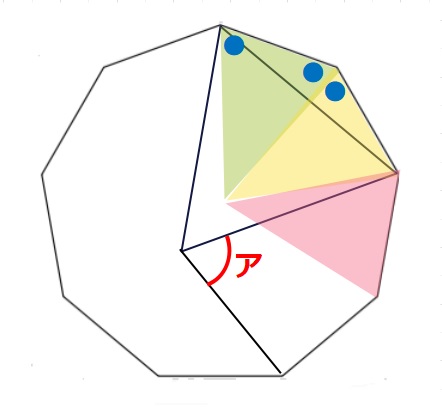
【ヒント】今回の問題ですが、いつものように対称な図形を意識して二等辺三角形をつくるとうまくいきます。オレンジの△DBFはDB=DFなので二等辺三角形となります。
また△DBAは正三角形なので、DB=DF=DAがわかります。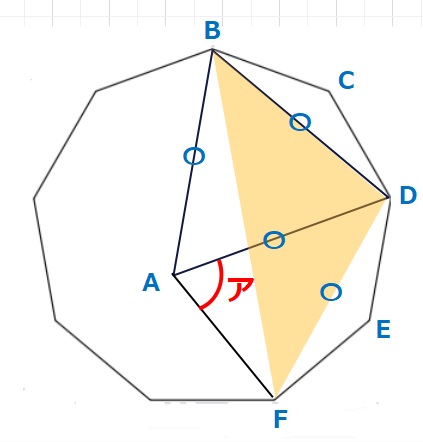
【解答】△CDBはCD=CBの∠BCD=140°の二等辺三角形なので、
∠CDB=\(\frac{180-140}{2}\)=20°
よって、∠BDF=140-(20+60+20)=140-100=40°
ア=∠DAF=\(\frac{180-40}{2}\)=70°・・・(答え)

コメント