難易度
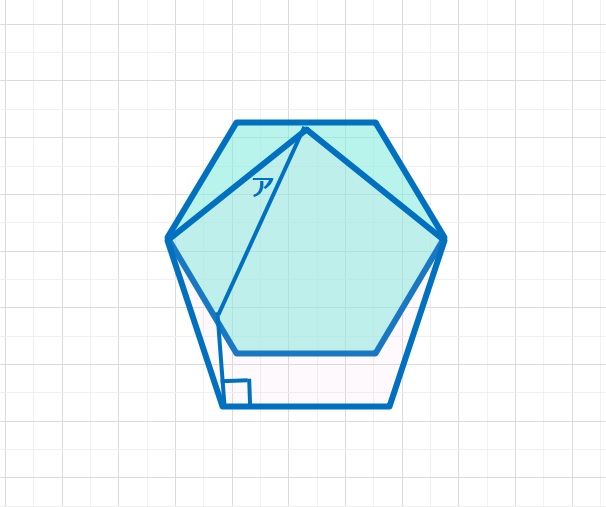
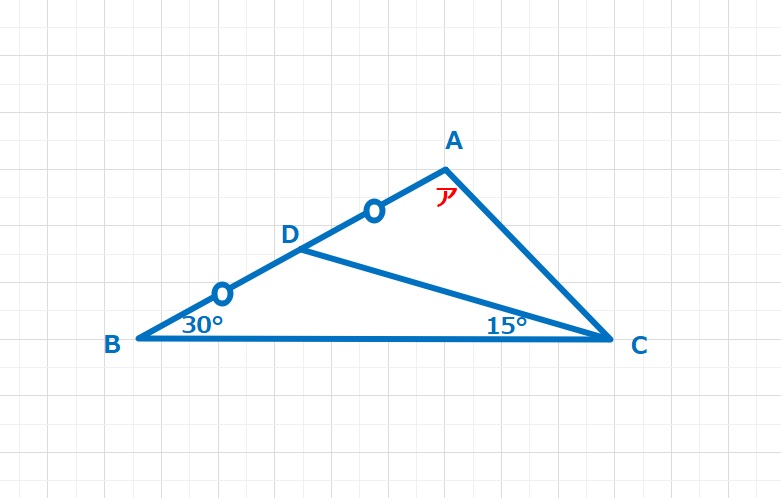
【問題】図のように正五角形と正六角形を組み合わせた図形があります。アの角度は何度ですか。
【ヒント】図のように使いそうな点に記号をつけておきます。正五角形と正六角形に注目してわかる角度を書き込んでいけば、とけると思います。(笑)ちなみに正五角形の1つの内角は120°,正五角形の1つの内角は108°ですね。計算してもよいですが、覚えてしまっている人も多いでしょう。
正五角形には、たくさんの練習問題を載せてますので、慣れてきたと思います。
情報量が多いので、1つ1つ丁寧に、確実に処理していきましょう。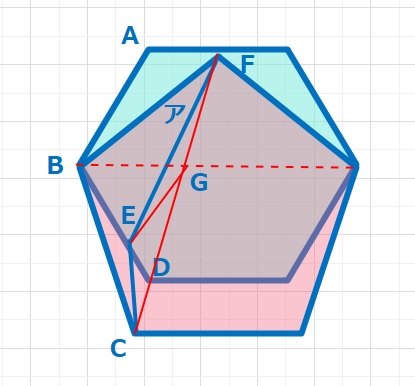
【解答】上図で△BCFは∠CBF=108°の二等辺三角形です。∠BCF=\(\frac{180-108}{2}\)=36°,また∠CBG=108-36=72°,正6角形の内角の半分である∠DBG=60°より∠CBD=12°
・△GBFに注目して、∠GBF=∠GFB=36°なのでGB=GF・・・①の二等辺三角形
・△CBGに注目して、∠CBG=∠CGB=72°なのでCB=CG・・・②の二等辺三角形
またBGとCIは平行で∠HCI=90°なので∠CHB=∠CHG=90°となります。
よって△EBGはEB=EG=BG・・・③の正三角形となります。
・△CBEと△CGEは 上の②③の条件とCEが共通なので三辺が等しく合同です。
よって∠BCH=∠GCH=18°,∠CBE=∠CGE=12°
・△GEFに注目して、①と③の条件よりGE=GFの二等辺三角形なので
∠EGF=180-12=168°,∠GFE=∠GEF=\(\frac{180-168}{2}\)=6°
ア=∠BFC-∠EFC=36-6=30°・・・(答え)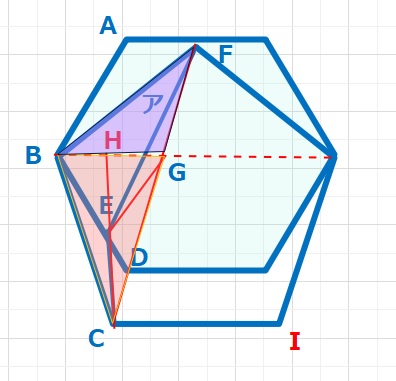
コメント