★★☆☆☆中級コース　腕試し問題　算数オリンピック問題より

難易度2.0
2008年　算数オリンピックトライアル（問１１）より
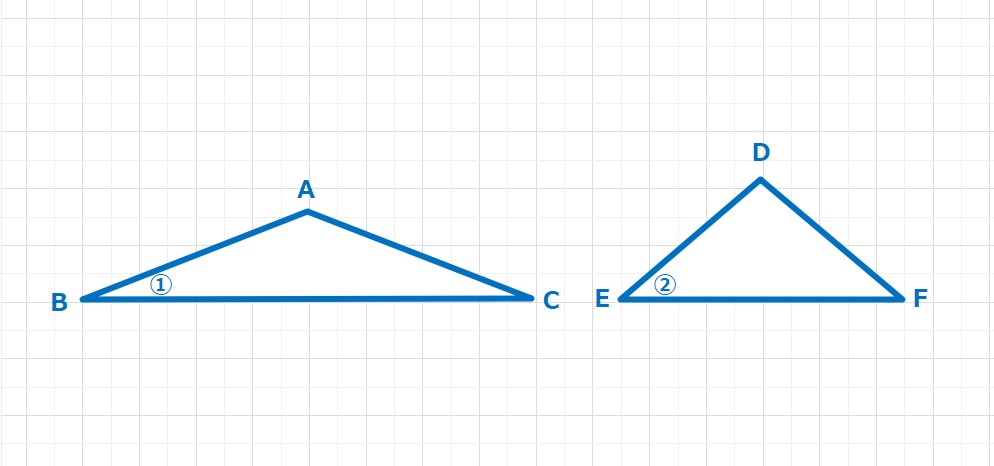
【問題】図の三角形ＡＢＣと三角形ＤＥＦは、ＡＢ＝ＡＣ＝ＥＦ、ＤＥ＝ＤＦ、ＢＣ＝ＡＢ＋ＤＥ、角ＤＥＦは角ＡＢＣの2倍です。この時、角ＡＢＣの大きさは何度ですか。

【ヒント】
ＡＢ＝ＡＣ＝ＥＦより下図のように組み合わせてみました。
三角形の外角の関係より、∠ＡＢＣ＋∠ＡＣＢ＝①＋①＝②＝∠CADとなりますので、
B,Ａ,Dは一直線上にあることがわかります。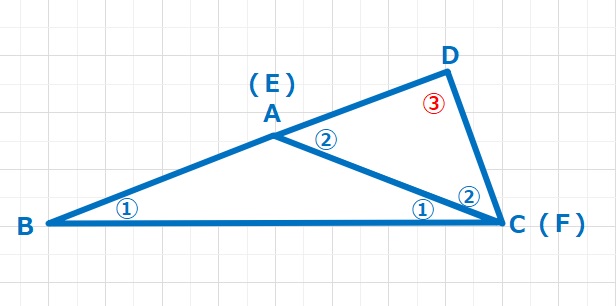

【解答】BC=BA+ADとB,A,Dは一直線上にあることより、BC=BDとなります。
　よって∠BCD=∠BDC=③となり、①＋①＋②＋③＝180°より⑦＝180°
　①は\(\frac{180}{7}\)ということがわかります。よって∠ABC=①＝\(\frac{180}{7}\)・・・（答え）