難易度
【ヒント】
∠BAD=90°に注目し、長方形BFDAとなるFを取る。
長方形ABFDの2つの対角線の交点をEとすると、AE=EF=BE=EDとなります。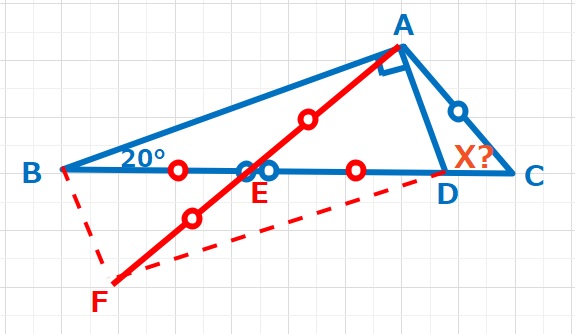
【解答】
長方形BFDAとなるF及び長方形の2つの対角線の交点Eをとる。
△EABにおいてEA=EBなので二等辺三角形。よって∠EAB=20°となる。また△AECにおいてAE=ACなので二等辺三角形となり、∠AEC=20+20=40°=X・・・(答え)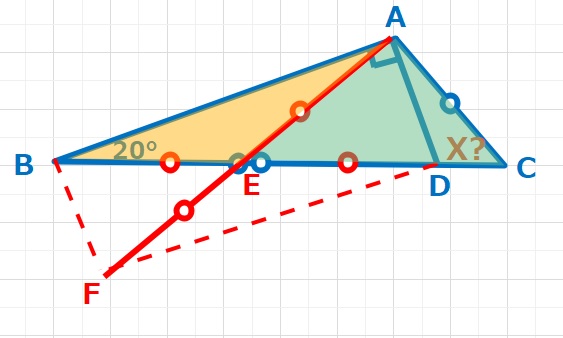
★★☆☆☆中級コース 長さをどう活用するかがポイント!
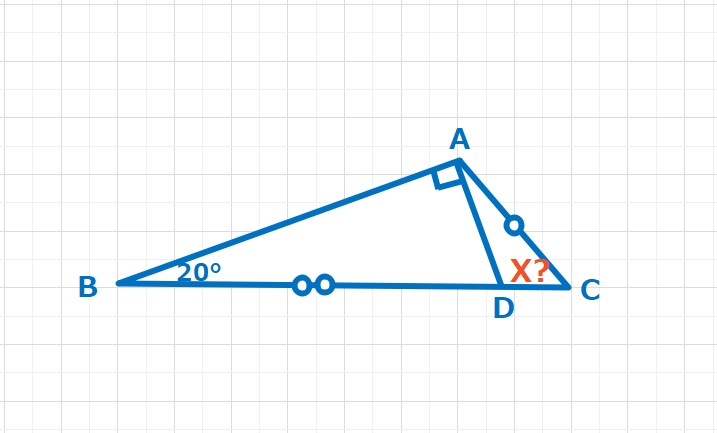 図形
図形 図形
図形難易度
【ヒント】
∠BAD=90°に注目し、長方形BFDAとなるFを取る。
長方形ABFDの2つの対角線の交点をEとすると、AE=EF=BE=EDとなります。
【解答】
長方形BFDAとなるF及び長方形の2つの対角線の交点Eをとる。
△EABにおいてEA=EBなので二等辺三角形。よって∠EAB=20°となる。また△AECにおいてAE=ACなので二等辺三角形となり、∠AEC=20+20=40°=X・・・(答え)
コメント