難易度
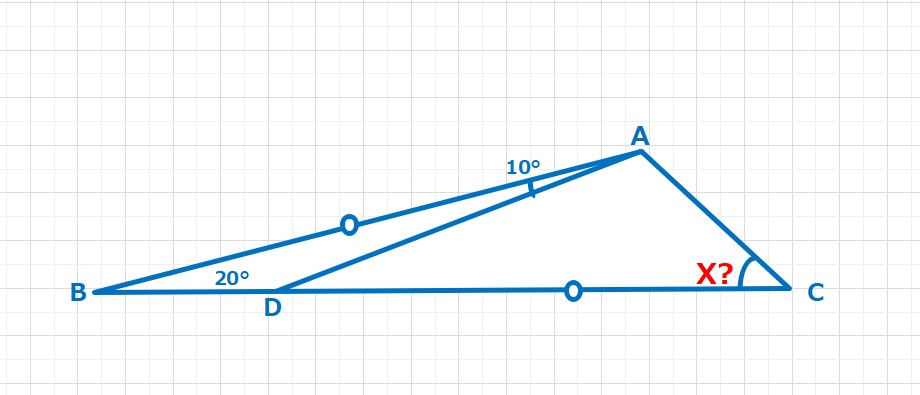
【問題】∠ABC=20°,∠BAD=10°,AB=DCのとき、∠ACBは何度ですか。
【ヒント1】以前取り扱いました、頂角20°の二等辺三角形の問題と似た問題になります。以前の問題が頭に入っている方は、すぐに解けるかもしれません。
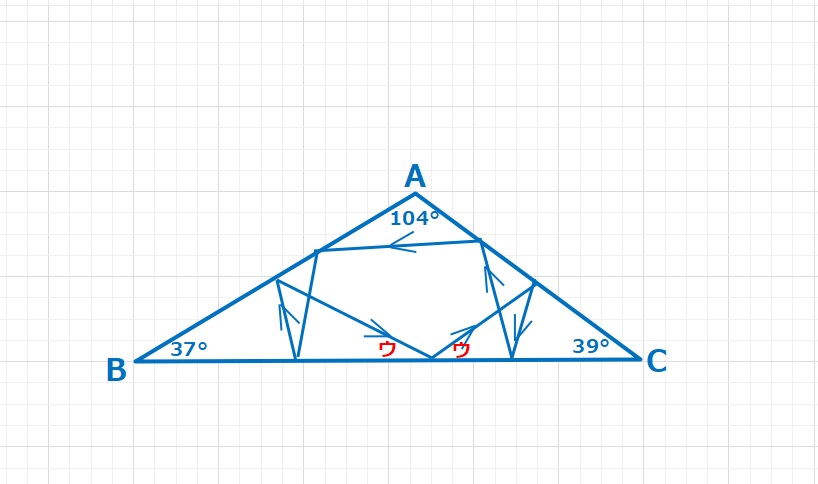
まずは△ABDをAB=DCを使って図のように、移動してみます。△DEA(ピンク)に注目すると、DE=DAなので△DEAは頂角40°の二等辺三角形となります。また△CEFも頂角20°の二等辺三角形となりますので、CE=CF=BDとなります。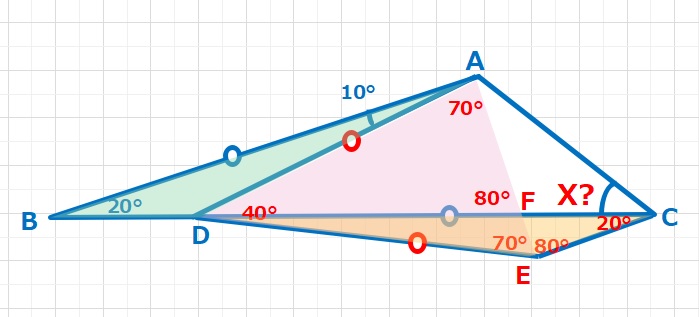
【ヒント2】次にAFを1辺とする△AFG(紫)を作ります。これは前回の頂角20°の二等辺三角形のところでも使用しました。△ABDと△BAGは1辺(AB共通)とその間の角(∠BAD=∠ABG=10°、∠ABD=∠BAG=20°)が等しいため、合同な三角形となります。よってBD=AG=GF=AFとなります。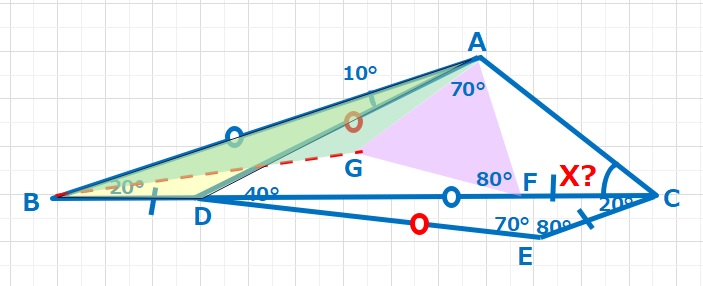
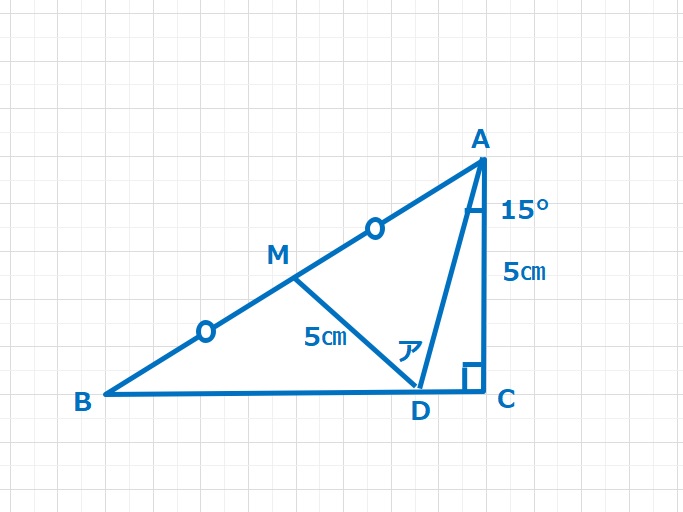
【解答】BD=EC=AEとなるため、△FACはFA=FCの二等辺三角形となります。また、∠AFC=100°なのでX=\(\displaystyle\frac{180-100}{2}\)=40°・・・(答え)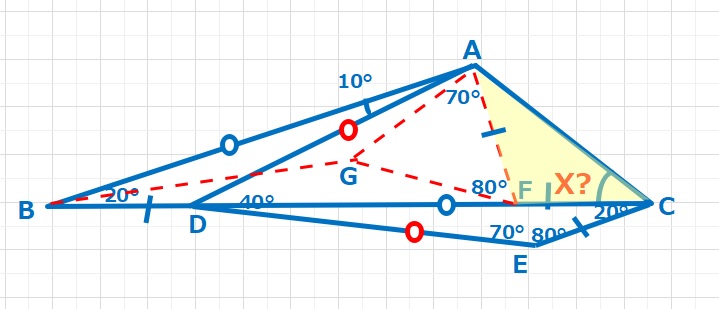
コメント