難易度
【ヒント】33+38=71であることに注目して。ADより38°傾いたAEをとると、∠ADE=∠AED=71°となり、△ADEは二等辺三角形でAD=AEとなる。また∠BAE=∠BEA=71°なので、△BEAも二等辺三角形で、BE=BAとなります。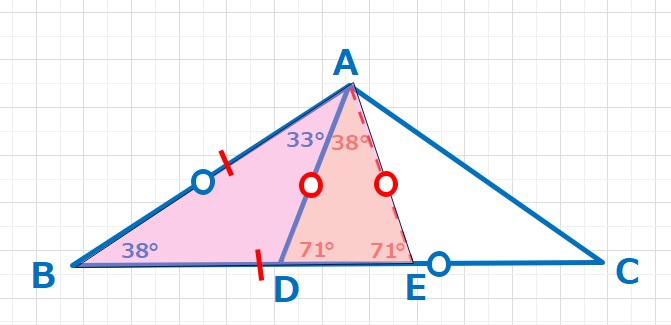
【解答】△ADBと△AECにおいて二辺(AD=AE,BD=(BE-DE)=(AB-DE)=(DC-DE)=EC)とその間の角(∠ADB=∠AEC=109°)が等しいので合同な三角形となります。よって∠CAE=∠BAD=33°となり、X=38+33=71°・・・(答え)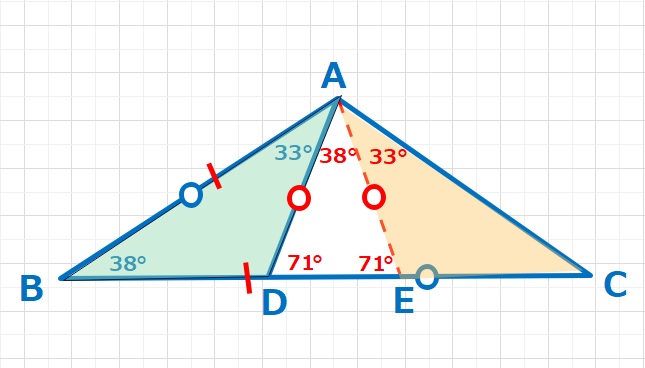
おまけ
私が最初に考えたのは、小学生の範囲を超えますが下記解法でした。いつものように△ABDを△CEDに移動させます。わかる角度を書き込んでいくと、∠DAE=∠DCE=38°ですので、四角形ADECは円に内接しています。よって∠CAF=∠CDF=33°となり、X=38+33=71°・・・(答え)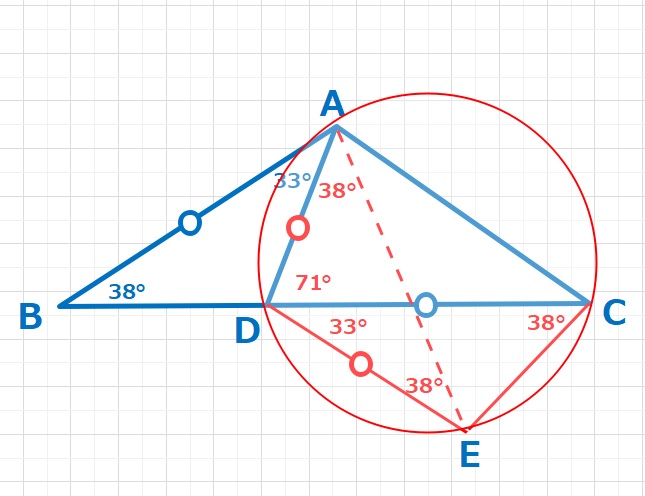
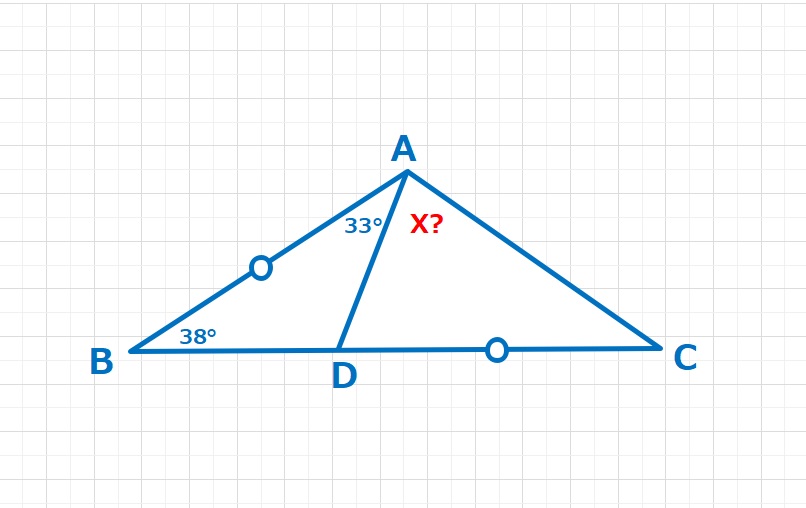
コメント