角度とはなにか?
角度とは角の大きさを表す量のことです。(算数の範囲では)角は2つの直線と直線が交わったときにできます。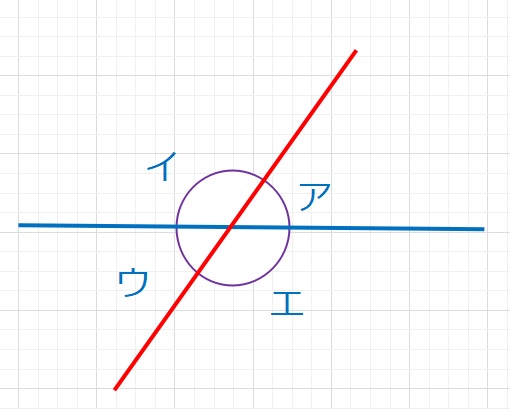
図のように2つの直線が交わった時、ア、イ、ウ、エの領域に分かれますが、この領域に対応して角があり、その大きさを表すものが角度です。アの角度とイの角度ではなんとなくアの角度の方が小さいことはわかると思います。
さて、これをなんとなくではなく、もう少し具体的に表現したいのですが、世界中で広く使われている単位-国際単位系-の単位としては数学で学ぶ、ラジアンというものがあります。
ラジアンとは別に、私たちの日常でよく使うものとして算数で学ぶ「度」というものがあり、「°」と表記します。度は円周を360等分した弧の中心に対する角度となります。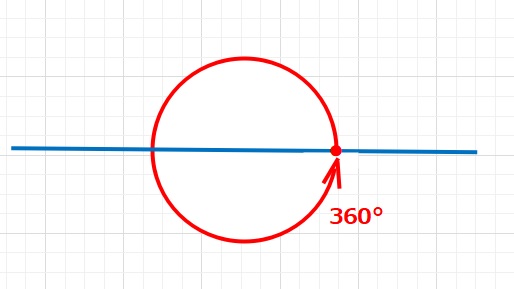
図のように1周回った角度(周角)は360°と表現できます。図では矢印を書いてますが、角度に方向はありません。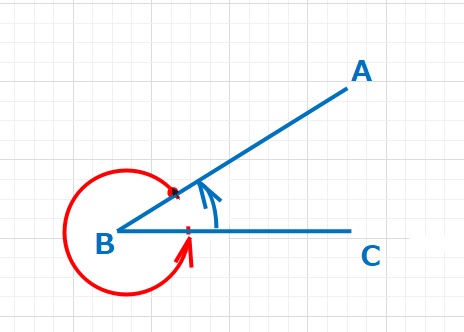
Bを共有する、線分ABとBCがあるときにできる角を角ABCと表現し、記号で∠ABCと書きます。その際に上図のように、角に方向はないので青の角と赤の角が存在しますが、小さくないほう(赤の方)の角を優角(ゆうかく)とよび、そうでないほう(青の方)を劣角(れっかく)と呼びます。優角と劣角の和は周角(一周まわった角)360°となります。通常なにも言わない場合、∠ABCといえば劣角(青の方)をさします。つまり劣角は0°から180°の間の角をさし、優角は180°から360°の間の角をさしますが、この言葉の使用頻度はさほど高くありません。ちなみに、角度が90°のとき直角といい、下図のように表記することがあります。また90°より小さい角を鋭角、90°より大きく180°より小さい角を鈍角ということがありますが、こちらもそれほど頻繁につかわれる言葉というわけではありません。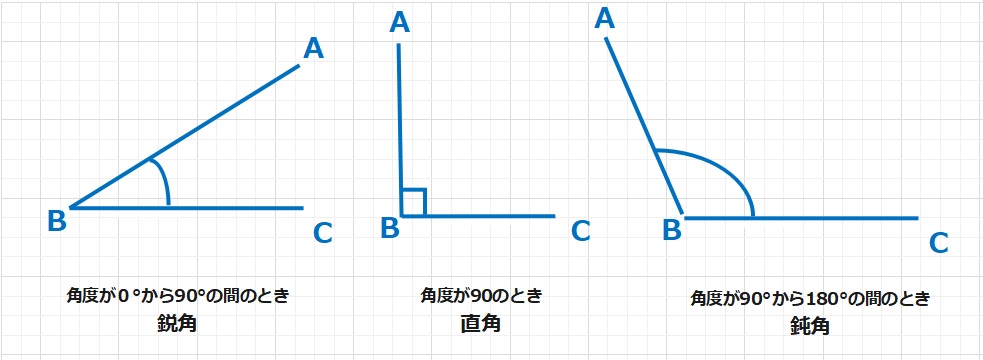
1°より小さい角度
それでは1°より小さい角度はどのように表現するのでしょうか。
10進法で小数点以下の数値を使用して度で表す方法、例えば30.75°のような方法が推奨されています。別の方法として、60進法を用いて1度を60等分した分や、1分を60等分した秒(1/3600度)を用いて、表現する方法があります。分は記号で「’」と表記し、秒は記号で「’’」と表記され、
20°14’34”のように表記します。算数では前者の10進法の表記を使用しています。
なお、60進法を用いる場合、秒よりも小さい単位もあるようですが、普通は秒以下は少数点を用いて表記することが一般です。秒より小さい単位に興味のある方は、ぜひ調べてみてください。
なぜ1周は360°?
これには諸説あるようですが、360という数は、古くは1年は360日で概算され、メソポタミア文明は30日×12周で、マヤ文明は20日×18周で概算されていたそうで、この1年の日数に由来するともいわれているようです。
また1周を360度とすることで、星が北極星を中心として1日1度回ることになり、星を観測する際に便利だったようです。これを幾何学における角度の測定に応用した人物は、ギリシャの7賢人の1人といわれている哲学者タレス(紀元前624年頃ー紀元前546年頃)であると考えられてます。
360という数字は約数が24個と比較的多く、とても割りやすい数で、10以下の正整数のうち、割り切れない数は7だけです。ちなみに10以下の全ての正整数で割り切れる最小の数は2520ですが、この数字は大きすぎるため、360°の方が実用的な目的において、十分な精度で表現するのに丁度よい角度であると考える人が多いようです。
【コラム】ゼロから始める 角・角度について考える
 コラム
コラム
コメント