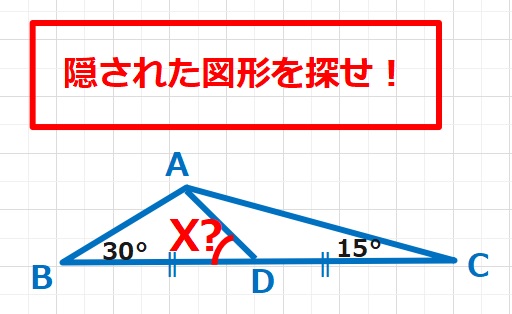
難易度
【ヒント】与えられた条件から、隠された図形をイメージすると・・・分かっている30°を活用して30°、60°、90°の直角三角形を作るか、15°を活用して、△ACDを折り返し、30°の二等辺三角形をつくる、とかが思いつきます。今回は、30°、60°、90°を作ってみました。
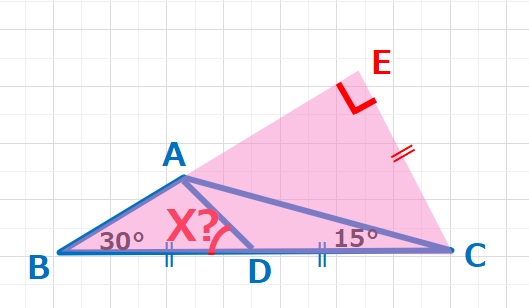
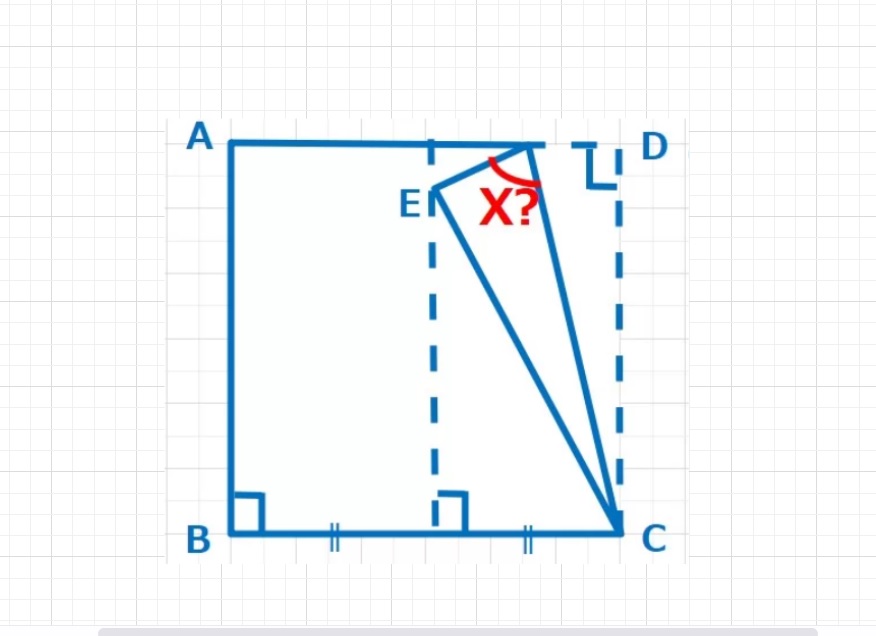
CからBAの延長線上に下した垂線をの交わる点をEとすると、BC:CE=2:1となるので、△BCEは30°、60°、90°の直角三角形となり、下図のようになります。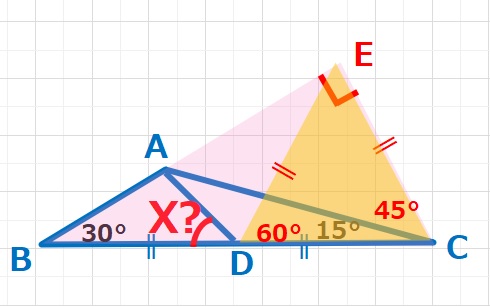
△ECAは45°、45°、90°の直角二等辺三角形となるので、EC=EAとなり、△EDAは 30°、75°、75°の二等辺三角形となります。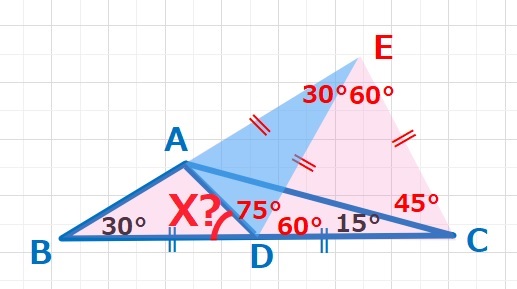
【解答】
BAの延長線上にCE=CDとなる点Eをとると△BCEは直角三角形となる。△EACは直角二等辺三角形となり、結果△EADは30°、75°、75°の二等辺三角形。
よってX=180ー(75+60)=180-135=45°・・・(答え)
コメント