1の位に5が入っているかけ算
【パターン1】□×2に変形できる(偶数)場合 18×35=?
5×2=10を作り出して、計算を簡単にします。
この例題の場合、18が2×9に分解できるので、うまくいきます。
35×(2×9)=(35×2)×9=70×9=630
【パターン2】□×2に変形できない(奇数)場合 9×35=?
この例題の場合、9=3×3と2が入っていないため、5×2がつくれません。
そんな場合は、いったん2をかけて最後に2で割ります。
9×35×2×\(\frac{1}{2}\)=9×70×\(\frac{1}{2}\)
=630×\(\frac{1}{2}\)=315
下2ケタに25が入っているかけ算
25が入っている場合は、25×4=100をうまく使います。
【パターン1】□×4に変形できる場合 36×25=?
36=9×4ですので、9×4×25=9×100=900と簡単に計算できます。
【パターン2】□×4に変形できない場合 37×25=?
37×4×25×\(\frac{1}{4}\)=37 ×100×\(\frac{1}{4}\)
=3,700×\(\frac{1}{4}\)=925
下2ケタに75が入っているかけ算
75=3×25を活用します。
【パターン1】□×4に変形できる場合 32×75=?
(8×4)×(3×25)=(8×3)×(4×25)=24×100=2400
【パターン2】□×4に変形できない場合 13×75=?
13×(3×25)×4×\(\frac{1}{4}\)=39×100×\(\frac{1}{4}\)
=3900×\(\frac{1}{4}\)=1950×\(\frac{1}{2}\)=975


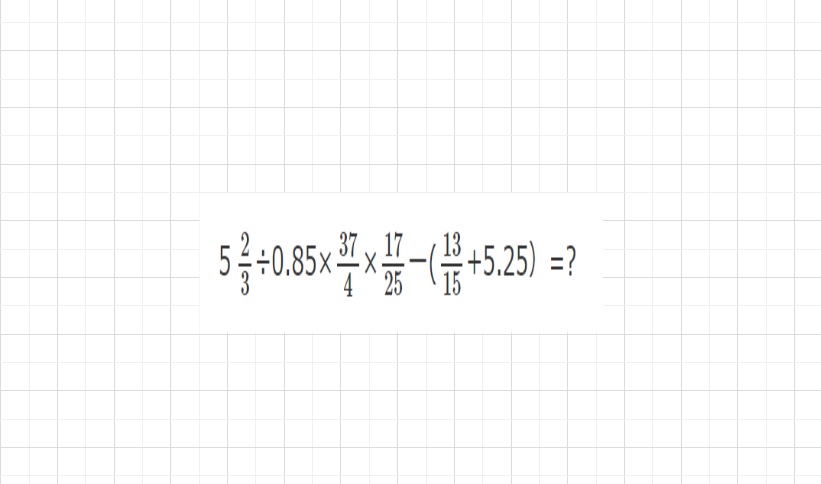
コメント