2021と2023を考える前に、まず素数とはなんでしょうか。
「1とその数以外に約数をもたない数」を素数といいます。
別の言い方をすると、1は素数でななく、「1以外で自分自身でしか割り切れない自然数」
を素数といいます。
素数をみつけるのに有名な方法として、エラトステネスの篩(ふるい)というものがあります。
まず、1から100まで数字をかいてみます。
・1は素数でなないのできえます。
・2は1と2しか約数を持たないので、素数確定です。
ということは、その後の2の倍数は素数ではないということになります。
図ではグレーで消しました。
・3は1と3しか約数を持たないので、素数確定です。
同様に、3の倍数は素数ではないのでさらに残ってるものをブルーで消しました
・次に残っている5は素数です。
5の倍数で残ってるものを紫で消します。
・次に7は素数です。同様に7の倍数をグリーンで消します。
・11は素数です。
ここで、100は10×10ですので、2,3,5,7,11でわりきれない100までの数字はすべて素数ということになります。
ということで、下の赤字の25個の数字が100までの数字の素数となります。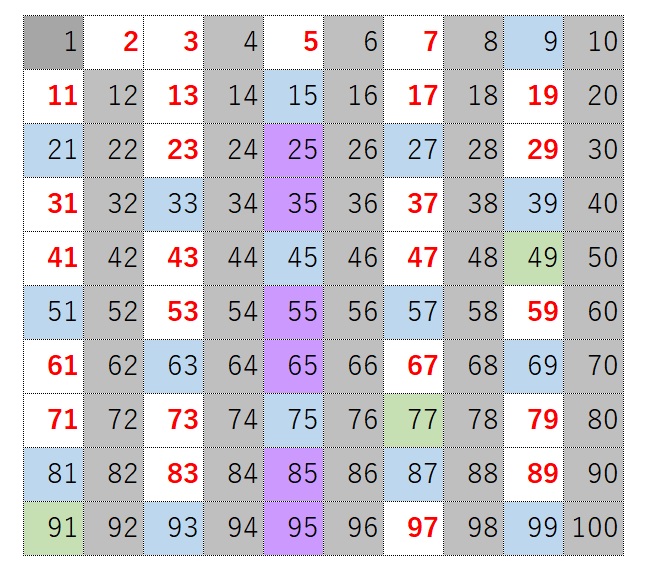
ここでやっと、問題の2021と2023について考えます。
やり方は100までの素数を探した方法と同じで、同じ素数をかけて2021と2023に近い数字をまずみつけます。ざっくり40×40=1600、50×50=2500なので40と50の間の素数だとわかります。
この素数は41、43、47、しかないですので41×41=1681、43×43=1849、47×47=2209となり、
2021と2023がそれぞれ2から47までの素数で割り切れなければ、素数となります。
◆まず2021。2から順番にずっとわっていきますが、最後に2021=43×47と43でわれました。
おしい!43で割れなければ素数確定なのですが、素数ではありませんでした。
◆2023は、同様にわっていくと、、、2023=7×289と7でわれました。
しかも289=17×17となりますので、2023=7×17×17と17でもわれました。
来年は2023年ですので、この数字はしっていると役に立つかもしれませんね。
数と計算の武器 素数とは? 2021 2023は素数か?
 数と計算の武器
数と計算の武器

コメント