約数とは
約数とは、ある整数をわりきることのできる整数のことです。
例えば、6の約数は、1,2,3,6となります。
約数の求め方
約数をもとめるには、その数を素数で表してみることが大切です。
すべての数は素数か素数の積で表すことができます。
これを素因数分解といいます。
例えば、168を素数で分解してみると、できる限り小さい素数2や3で割ってみます。
2で割ると、84。まだ2で割れて42。まだわれて21。ここで3で割れて7となり
7は素数ですのでこれ以上われません。
以上により168=2×2×2×3×7と表すことができます。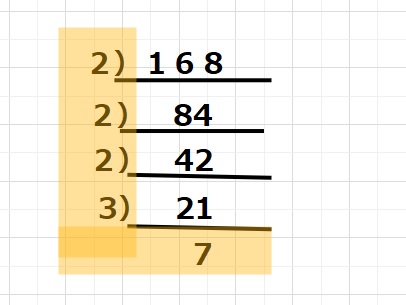
同じ数(文字)を何度もかける表現方法(累乗<るいじょう>)
同じ数を何度もかける計算を表記するー例えば、11を100回かける時、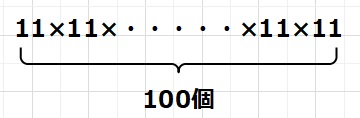
と何度も表現するのは、とても大変です。
そんな時、決め事として、\(11^{100}\) と書き、11の100乗と呼んでいます。
これは算数では出てきませんが、とても便利なので是非使ってほしいです。
ちなみに、\(11^{0}\) は1で、0乗はどんな数字でも1となります。
約数の個数を求める
約数の個数は素因数分解できればすぐにわかります。
先ほどの例で168は
「2」が3個含まれています。
よって2を0個使う、1個使う、2個使う、3個使うの4通りが考えられます。
次に3が1個含まれてますので、0個、1個の2通りが考えられます。
同様に7が1個含まれるので、0個、1個の2通りが考えられます。
これらをくみあわせると、4×2×2=16通りが考えられ、これが約数の個数です。
約数の総和を求める
同様に168で考えると
約数の総和は (1+2+4+8)×(1+3)×(1+7)と表現できます。
15×4×8=30×4×4=16×30=480となります。
ちなみに約数は 1,168 2,84 4,42 8,21 3,56 6,28 7,24 12,14 の16通りと
なり、先ほどの計算と同じ数になります。このようにペアで書きだすと抜け漏れが
少なくなります。
約数の数からわかること
約数が1個となる場合は1。
約数が2個となる場合は素数。
約数が3個となる場合は素数の平方数 2×2 3×3 5×5など
約数が4個となる場合は素数を3回かけた数 2×2×2などか 素数A×素数B 3×7など
約数が奇数個となる場合は平方数 2×2 4×4 8×8など
約数の和と約数の逆数の和の関係
6を例に考えてみます。
6を素数に分解すると、2×3となり、約数は1,6 2,3の4個となります。
約数の逆数は、1,\(\displaystyle\frac{1}{6}\),\(\displaystyle\frac{1}{2}\),\(\displaystyle\frac{1}{3}\) となり、
逆数の和は、\(\displaystyle\frac{6+1+3+2}{6}\)となります。
分子は約数の総和となっていますので、約数の逆数の和は、約数の総和を与えられた数で割った数と等しくなるといえます。
これはとても興味深いです。
最大公約数と最小公倍数
共通の約数を公約数といい、その中で最も大きな公約数を最大公約数といいます。
共通の倍数を公倍数といい、その中で最もちいさな倍数を最小公倍数といいます。
この求め方は、両方ともほぼ同じ方法ですのでいっしょにご紹介します。
【例】24 72 36 という数字があります。この最大公約数と最小公倍数を求めるには、
先ほどご紹介した約数を見つける方法と同じやりかたでさがします。
前回とちがうのは、すべてでわれる素数を見つけるということです。
今回2でわると、12 36 18となりますのでもう1回2でわれます。
さらに3でわれそうです。 2 6 3が残り、これ以上すべてで割れる数字はなさそう
なのでここで終了です。
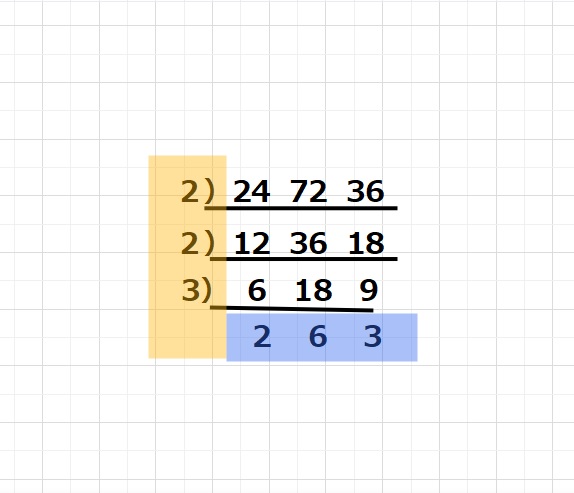
このひっ算の オレンジ部分のかけ算、2×2×3=12が最大公約数で、
オレンジとブルーすべてのかけ算 2×2×3×2×6×3=432が最小公倍数となります。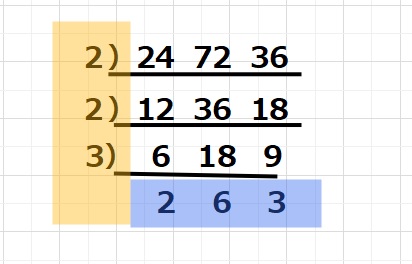


コメント