かけ算の基本的な考え方 1の位が小さい2ケタのかけ算
かけ算は下図のように「かけられる数」をたてに、「かける数」を横に
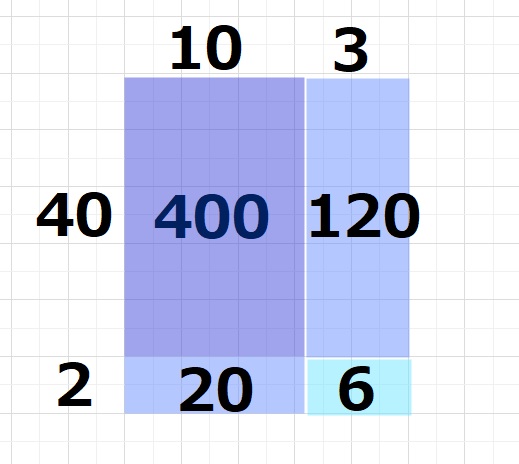
下2ケタ目と下1ケタ目1を分解して書くと、面積(広さ)と同じになります。
①40×10=400
②40×3=120
③10×2=20
④2×3=6 を計算してすべてをたすと、
400+120+20+6=546となります。
この考え方が、かけ算の基本的な考え方となります。
1の位が大きい2ケタのかけ算
【例題】32×19=?
上で説明したとおりにやってみると、下図のようになります。
300+270+20+18=608と計算できますが、
2つ目の図のように計算する方が、少し簡単です。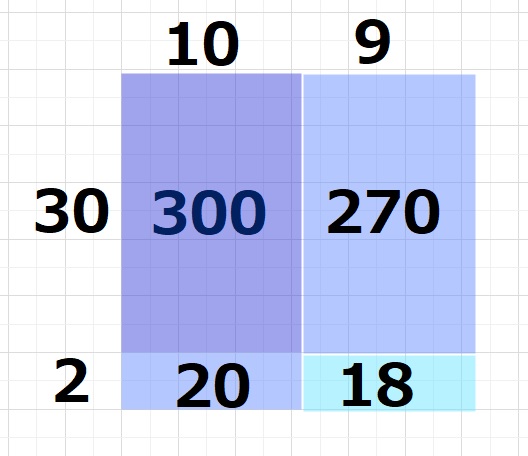
かける数(よこ)の数字を10と9に分けるのではなく、キリのよい20と1
にわけて、余分に青の面積 600+40をまず計算し、
そのあとで、赤の面積 30+2をひくという方法です。
こちらの方が基本の求め方よりも少しだけ楽に計算できます。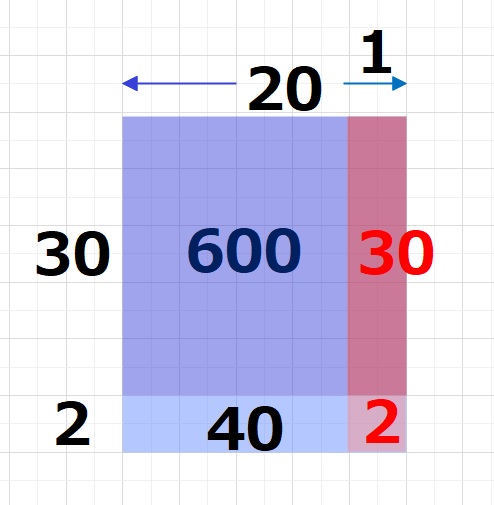
1の位が2つとも大きい2ケタのかけ算
【例題】98×97=?
98をきりのよい100と2に、97を100と3にわけて、
青色の面積100×100=10000を求めて、赤色の面積をひきます。
200+300をひくと、6の部分を2回ひくことになりますので、
10000-500=9500に引きすぎた6をたして9506となります。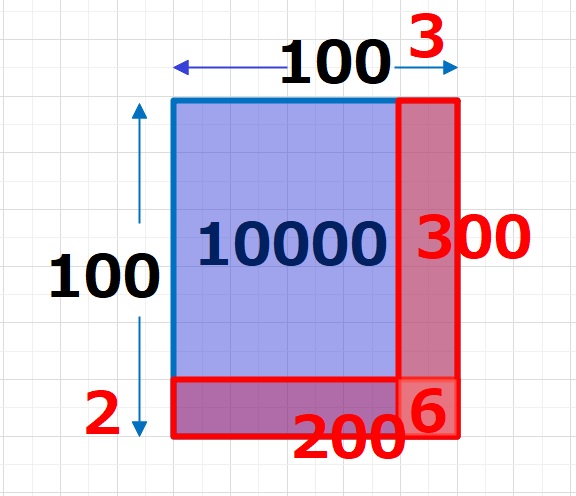


コメント