★★★☆☆難関コース　面積の問題。2015年　開智未来中学入試問題。

難易度3.0
2015年　開智未来中学校入試
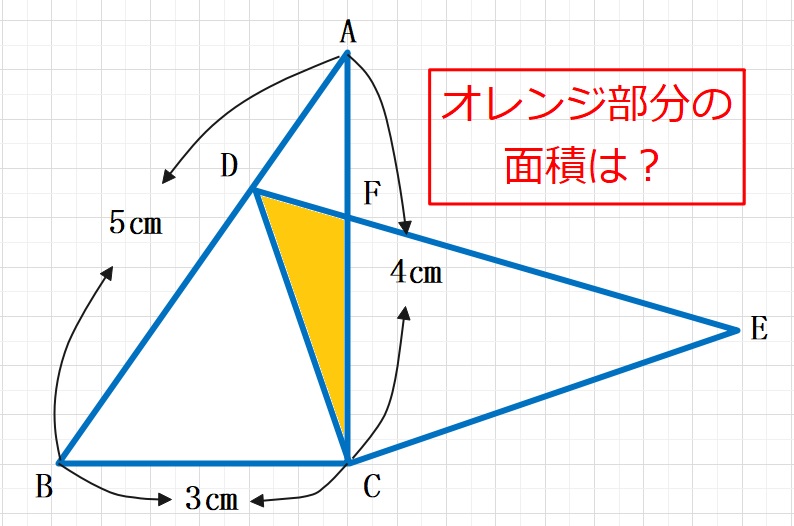
AB=5㎝,AC=4㎝,BC=3㎝の直角三角形ABCがあります。△ABCをCを中心に回転した三角形が△EDCです。△CFDの面積を求めなさい。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

ヒント
△ABGと△CEA ,△CDBは相似な二等辺三角形となります。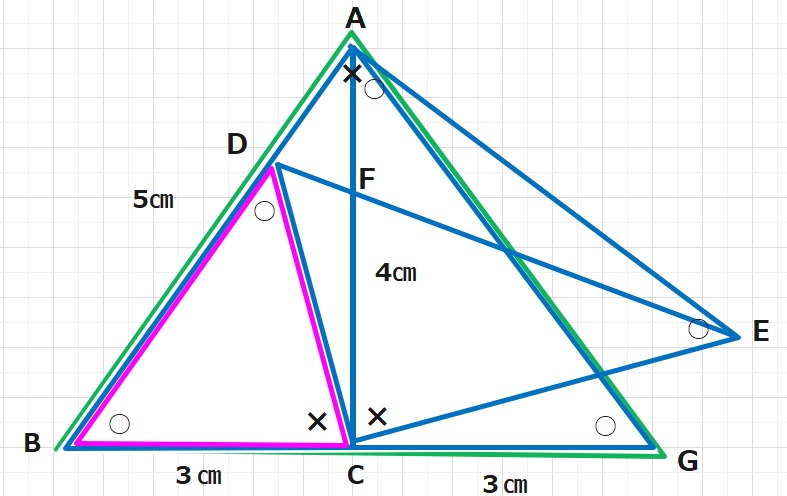

【解答】△ABC＝\(3\times4\div2\)＝6㎠, △ABG＝\(６\times２\)＝12㎠
△ABG：△CDB＝12：△CDB＝\(5\times5：3\times3\)なので、　・・・ポイント①
△CDB＝\(\displaystyle\frac{108}{25} \) 　　　△DAC＝6ー\(\displaystyle\frac{108}{25}\)=\(\displaystyle\frac{42}{25}\)
また、△ABG：△CEA＝12：△CEA＝\(5\times5：4\times4\)なので、
△CEA＝\(\displaystyle\frac{192}{25 }\)
△CBD：△CDA：△CEA = 108：42：192 = 18：7：32
DF：FE = △CDA：△CEA = 7：32　　・・・ポイント②
△EDC = △ABC=6㎠　なので
△FDC ＝ \(\displaystyle\frac{７}{39}\)\( \times6\) ＝ \(\displaystyle\frac{14}{13}\) ＝ 1\(\displaystyle\frac{1}{13}\)

ポイント①　相似な三角形の面積比
ポイント②　高さが同じ三角形の面積比