2021年 開成中学入試問題より
【問題】三角すいの体積は、(底面積)×(高さ)÷3で
求めることができます。
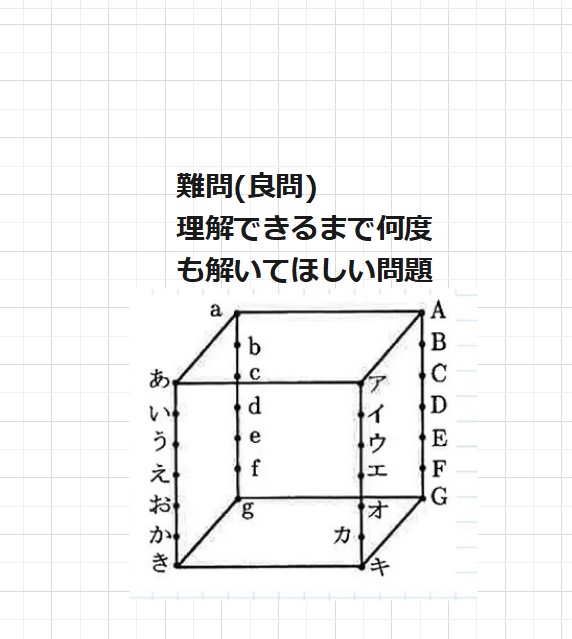
1辺の長さが6cm の立方体の平行な4本の辺を
それぞれ6等分し、下の図のように記号を付けました。以下の問に答えなさい。
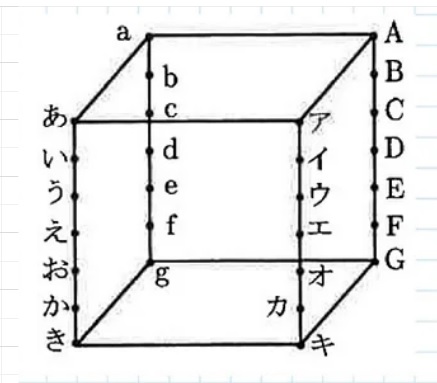
(1)4点き、G、a、gを頂点とする
三角すいの体積を求めなさい。
(2)4点き、ウ、G、aを頂点とする
三角すいの体積を求めなさい。
(3)4点い、オ、C、gを頂点とする
三角すいの体積を求めなさい。
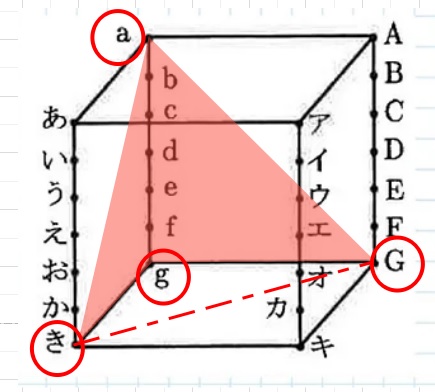
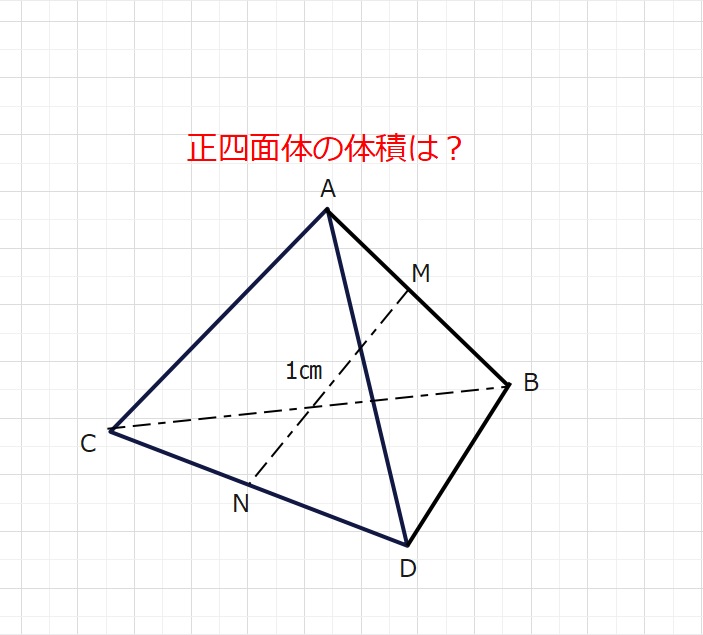
【1のヒント】下図の通り、三角形gきGを底辺とすると、高さがagの
三角すいとなっています。
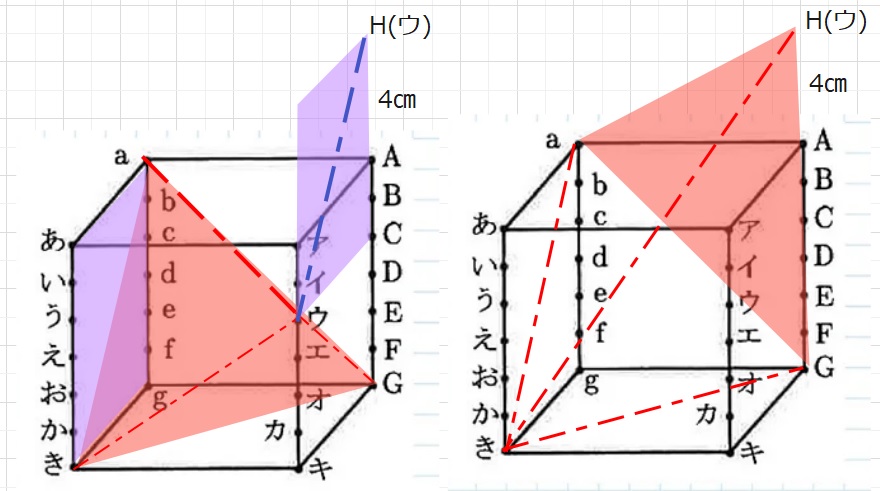
【2のヒント】等積変形の考え方を活用します。
平面あきgaと平行な平面アキGAを考え、点ウをAG上に移動します。
紫の面を比較し、点ウは点Hに移動できます。
求める体積は、き-GHaの体積と同じになります。
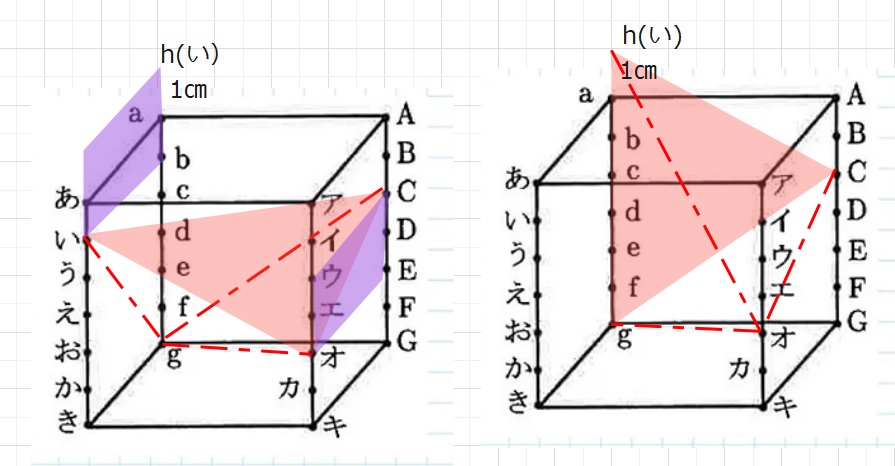
【3のヒント】2と同様、等積変形の考え方を使います。
平面アキGAと平行な平面あきgaを考え、点いをag上に移動します。
紫の面を比較し、点いは点hに移動できます。
求める体積は、オーCgaと同じになります。
【解答】
(1)6×6×\(\displaystyle\frac{1}{2}\)×6×\(\displaystyle\frac{1}{3}\)=36㎤・・・(答え)
(2)10×6×\(\displaystyle\frac{1}{2}\)×6×\(\displaystyle\frac{1}{3}\)=60㎤・・・(答え)
(3)7×6×\(\displaystyle\frac{1}{2}\)×6×\(\displaystyle\frac{1}{3}\)=42㎤・・・(答え)

コメント