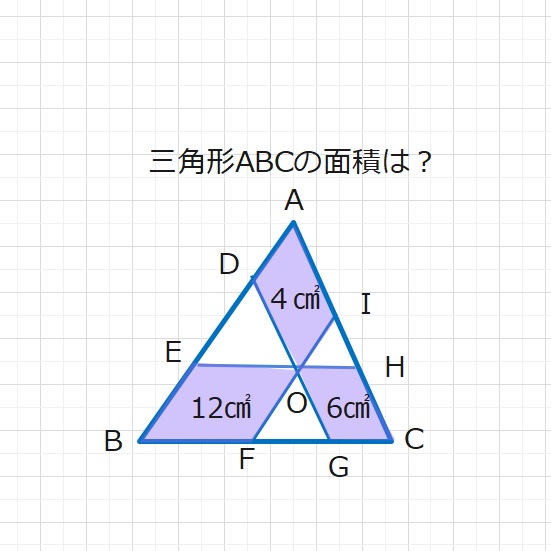
【問題】三角形の中にある点Oを通り、AB、BC、CAに平行な直線
IF、EH、DGがあります。図の3つの平行四辺形の面積がそれぞれ
4、12,6㎠のとき、三角形ABCの面積はいくつですか。
【ヒント】平行四辺形EBFOと平行四辺形OGCHの面積は12㎠、6㎠より
BF:GC=12:6 =2:1
また、平行四辺形ADOIと平行四辺形HOGCの面積は4㎠、6㎠より
DO:OG=4:6=2:3
相似な三角形、△DEOと△DBGに注目して、EO:BG=2:5
EO=BFより BF:FG:GC=2:3:1となります。
三角形OFGと平行四辺形OGCHの高さは等しいので、
2つの図形の面積比がわかります。
これより△OFGの面積がわかり、四角形EBCHの面積がわかります。
また相似な三角形AEHとABCよりEH:BC=(EO+OH):BC=3:6=2:1
となり、面積比は △AEH:△ABC=1×1:2×2=1:4となります。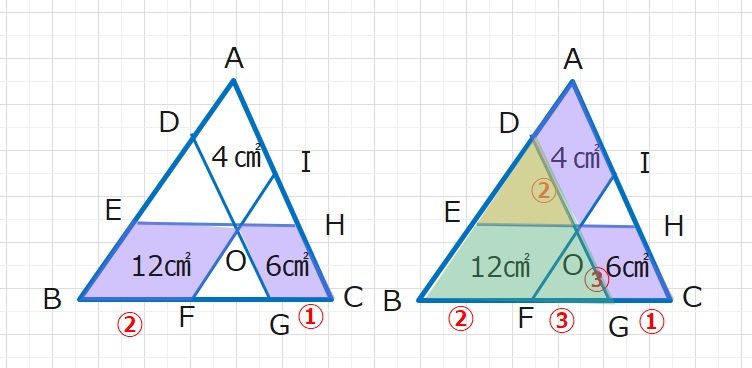
【解答】
三角形OFGと平行四辺形OGCHの高さは等しく、FG:GC=3:1なので
面積の比は3:2になります。平行四辺形OGCH=6㎠なので、
△OFG=\(\displaystyle\frac{6×3}{2}\)=9㎠
相似な三角形AEHとABCよりEH:BC=(EO+OH):BC=3:6=2:1
となり、面積比は △AEH:△ABC=1×1:2×2=1:4
よって△ABC:四角形EBCH=4:3=△ABC:27㎠
△ABC=\(\displaystyle\frac{4×27}{3}\)=36㎠・・(答え)
コメント