2021年 渋谷教育学園学渋谷中学入試問題より
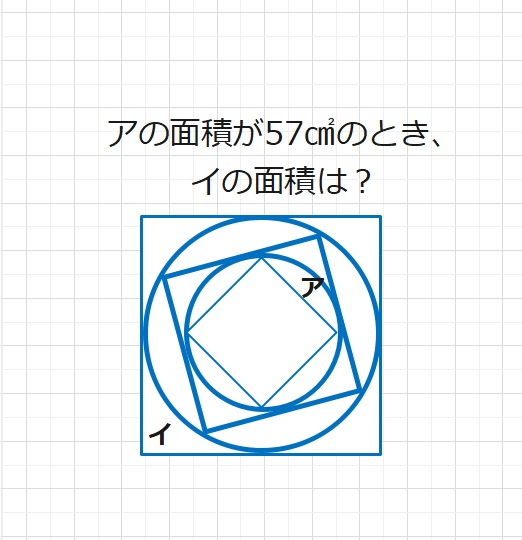
【問題】正方形と円からできている図について、アの部分の面積が57㎠のとき
イの部分の面積は何㎠ですか。
【ヒント】
分かりやすくするために、正方形を下の図のように回転します。
黄色の直角二等辺三角形と緑の直角二等辺三角形は2:1の相似な三角形の
関係にあります。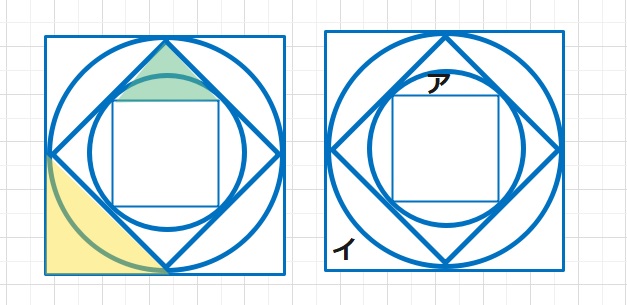
今、下図の正方形の1辺を1とすると、正方形の面積は1で
その半分の白い部分の直角二等辺三角形の面積は\(\displaystyle\frac{1}{2}\)
赤い図の面積は円の\(\displaystyle\frac{1}{4}\)の扇形から直角二等辺三角形の面積
を引いた面積となるので、
3.14×1×1×\(\displaystyle\frac{1}{4}\)-\(\displaystyle\frac{1}{2}\)
=3.14×\(\displaystyle\frac{1}{4}\)-\(\displaystyle\frac{1}{2}\)
=\(\displaystyle\frac{1}{4}\)×(3.14-2)=\(\displaystyle\frac{1}{4}\)×1.14
=\(\displaystyle\frac{1}{2}\)×0.57となります。
つまり、(赤の面積):(白の直角二等辺三角形の面積)=57:100
となります。この事実をしっていればすぐに解けますが、知らないでも問題ありません。
今回 アの面積は57となってますので、緑の三角形の面積は100となります。
ここで、もう一度、回転させた正方形の図をみています。
黄色の三角形は緑の三角形の2倍の関係にあるので、イの部分の面積は求まりそうです。
【解答】
アの面積が57なので、緑の部分は100㎠となります。
よって ウの面積は 100-57=43㎠となります。
今 黄色:緑=2:1なので、 エ:ア=イ:ウ=2:1となり
イの面積は ウの2倍、43×2=86㎠・・・(答え)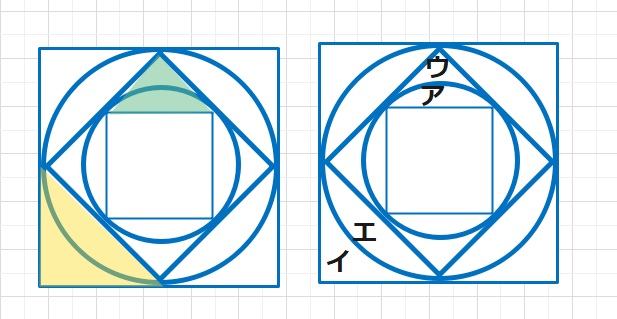
コメント