1998年 ジュニア算数オリンピックトライアル
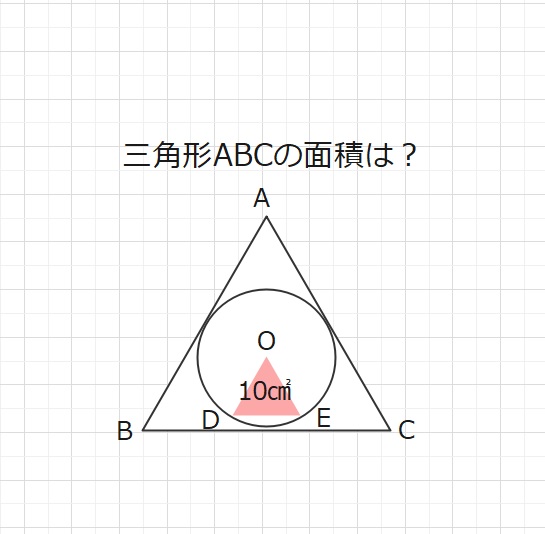
【問題】三角形ABC,三角形ODEは正三角形で、点Oは円の中心です。三角形ODEの
面積が10㎠のとき、三角形ABCの面積は何㎠ですか。
【ヒント】
下図のように円に内接する正六角形をイメージします。
紫の正六角形は赤の正三角形6個分です。
下の右図のように、正六角形を回転させると、黄色の正三角形は
紫の正六角形の\(\displaystyle\frac{1}{2}\)となります。
三角形ABCは黄色の正三角形4個分ですので、三角形ABCは紫の正六角形2個分です。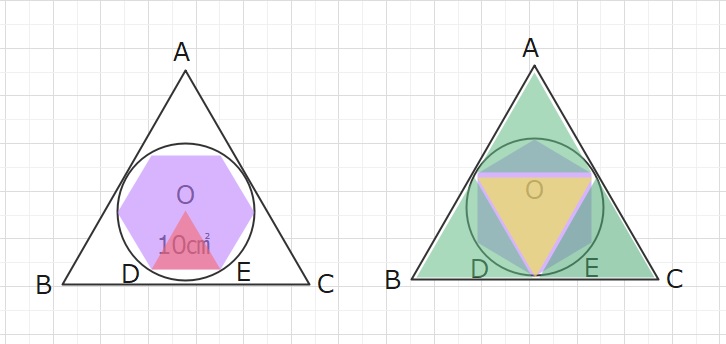
【解答】
三角形ABCの面積は正六角形2個分となり、正六角形は黄色の三角形2個分なので、
三角形ABCは黄色の三角形4個分となります。黄色の三角形は赤の三角形3個分なので、
三角形ABCは赤の三角形12個分、つまり12×10=120㎠・・・(答え)
コメント