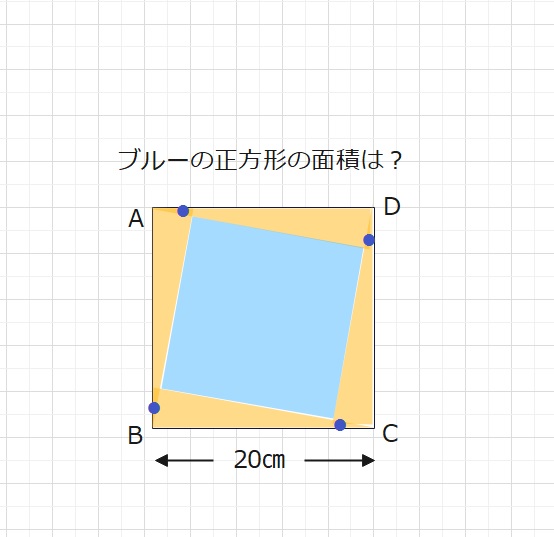
【問題】1辺が20㎝の正方形ABCDのなかに、オレンジの直角三角形を敷き詰めました。4つの●はすべて15°です。そのときブルーの正方形の面積はいくつですか。
【ヒント】
∠AEB+●=90°ですので、△BAEは∠BEA=90°、∠ABE=15°の直角三角形となります。
また△BAEと△AHD,△DGC,△CFBは合同な三角形となります。
ブルーの正方形の面積は、正方形ABCDから△BAE×4を引いたものとなります。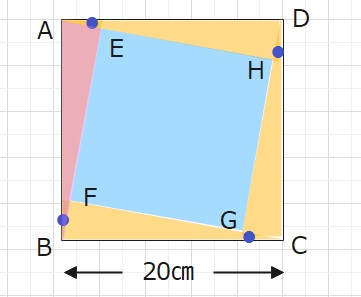
また15°の直角三角形を2つ組み合わせると、30°の二等辺三角形ができます。
30°の二等辺三角形は下の右図のように側面の辺の長さ(図では②)がわかれば、
図のようにして面積を求めることができます。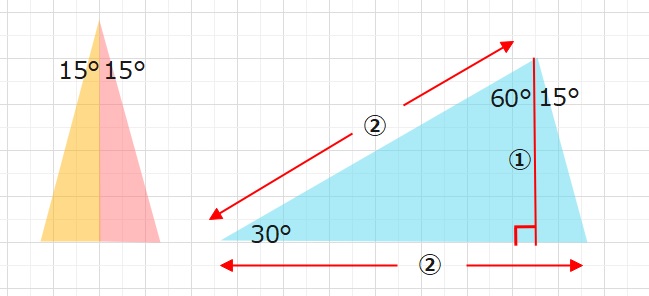
【解答】
△BAEを2つ組み合わせると、側面の辺の長さが20㎝、頂角が30°の二等辺三角形となります。
よって面積は、20×10×\(\displaystyle\frac{1}{2}\)=100㎠となります。
正方形ABCDの面積は20×20=400㎠
△BAE×4=100×2=200㎠ なので
求めるブルーの面積は400-200=200㎠・・・(答え)
コメント