2018年 開成中学入試問題より
【問題】正方形のマスの中に、1は1個、2は2個、3は3個のように整数nはn個使い
ある整数から連続した3種類以上の整数を図のように小さい順に並べます。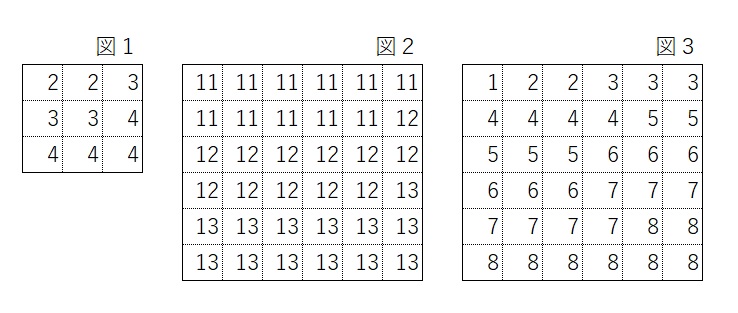
図1では3マス四方の正方形に2を2個、3を3個、4を4個ちょうど並べ切りました。
図2、図3では6マス四方の正方形に11から13まで、1から8までの整数をちょうど
並べ切りました。(6マス四方にならべる並べ方はこの2通り以外ありません)
次の問いに答えなさい。(1)(2)では2通り以上の並べ方がある場合は、すべて
答えること。解答欄には図1の3マス四方なら、2~4、図3の6マス四方なら
11~13、1~8のように書きなさい。
(1)7マス四方の正方形にちょうど並べ切るには、いくつからいくつまでの整数をならべればよいですか。
(2)10マス四方の正方形にちょうど並べ切るには、いくつからいくつまでの整数をならべればよいですか。
(3)30マス四方の正方形にちょうどならべきる並べ方は何通りありますか。またそれぞれの並べ方は何種類の整数を整数を使うか求めなさい。6マス四方の正方形にちょうど並べ切る並べ方は、図2図3の11から13、1~8の2通りです。この場合「2通りの並べ方があり、それぞれ3、8種類の整数を使う」と答えること。また種類を示す整数は小さい順に並べること。
【ヒント】問題が長いですが、一回経験したことがある人にとっては簡単な問題です。
連続する整数の和は「その数の1を除く奇数の約数の数だけある」ことと
連続する整数の和=①「平均」×「個数」若しくは②「連続2数のセットの数字」×「セット個数」
であることを理解していればすぐに解けます。
例題の6マスは6×6=36を連続する整数の和で表すことを参考にします。
36=2×2×3×3となり、約数は1,36,2,18,3,12,4,9,6の9個あります。
そのうち1以外の奇数は3と9の2つになります。
36=3×12と9×4と表現できます。
①3×12の場合 平均12で3個と考えると 11,12,13となります。
連即2数セット3を中心に12セットは存在しないので、上記のみです。
②9×4の場合 平均9で4個と考えると真ん中の数字がないので存在しません。
全族2数セットの数9(4,5)を中心に4セットとかんがえると残り3セットで
1,2,3,4,5,6,7,8となります。
これが問題に与えられたルールですが、背景を知っている人はスムーズに解けると思います。
【1の解答】7マス=7×7=49の約数は1,49,7となり、2通りありそうです。
49=7×7 か1×49
①平均が7を中心に7個の場合、4,5,6,7,8,9,10となります。
連続2数セットが7(3,4)を中心に7セットは存在しません。
②平均が49が1つのパターンは存在しません。
連続2数セットが49(24,25)が1セットはありますが、今回の問題では3種類以上の整数を使うので、該当しません。
よって、4~10・・・(答え)
【2の解答】10マス=10×10=100の約数は1,100,2,50,4,25,5,20,10の9個の約数のうち1以外の奇数は5と25の2通りです。
①100=5×20の場合、
平均20が5個と考え、18~22が該当します。
②100=25×4の場合、
平均25が4個は存在しないので、連続する2数セットが25(12,13)を中心に4セットと考え、9~16が該当します。
よって 18~22と9~16・・(答え)
【3の解答】30マス=30×30=900の約数は1,900,2,450,3,300,4,225,5,180,6,150,9,100,10,90,12,75,15,60,18,50,20,45,25,36,30,
の27通りありそのうち1以外の奇数は3,225,5,9,75,15,45,25の8通りがあります。
3の場合は平均300を中心に3個。
5の場合は平均180を中心に5個
9の場合は平均100を中心9個
15の場合は平均60を中心に15個
25の場合は平均36を中心に25個
45の場合は(22,23)を中心に20セットなので40個
75の場合は(37,38)を中心に12セットなので24個。
225の場合は(112,113)を中心に4セットなので8個。
以上を並べ替えると、
8通りの並べ方があり、それぞれ3,5,8,9,15,24,25,40個の整数を使う・・・(答え)となります。


コメント