2023年 灘中入試問題より
【問題】
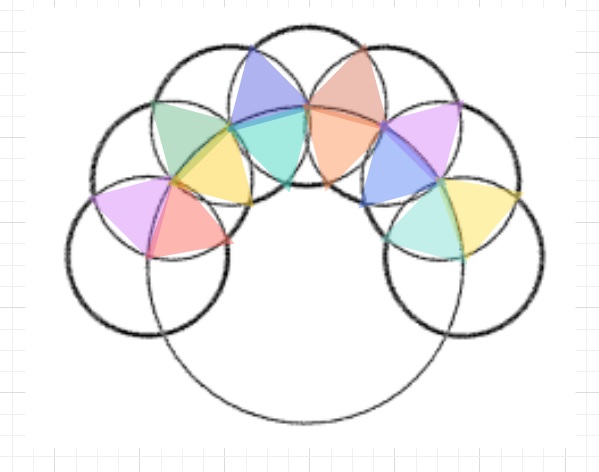
図のように、半径が2cmの大きな円の周上に中心を持つ、
半径が1cmの小さな円が7つあります。
また、小さな円の中心はその隣の小さな円の周上にあります。
このとき、太線の長さはアcmです。
【ヒント】
1辺が1㎝の正三角形が隠れていることにきづけば、ほぼ解けたようなものです。
このことにどれくらいの時間で気づくかが勝負です。
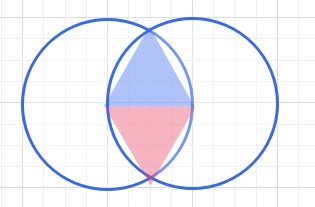
わかりやすく、書くとしたの円の外回りの長さは、2つの円の長さから、
120°のおうぎ形の弧の長さを2つ、つまり240°のおうぎ形の弧の長さを引いたものとなります。
【解答】求める長さは、7個の円周の長さから、120°×12=1440° 1440=360×4なので
7個分の円周から4個分の円周を引いたもの、つまり3個分の円周となります。
2×3.14×1×3=18.84㎝・・・(答え)


コメント