2023年 灘中入試問題より
【問題】
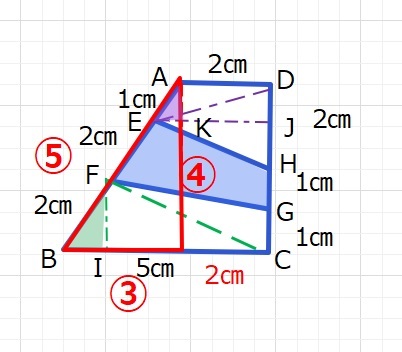
図のように,四角形ABCDの辺上に点E,F,G, Hがあります。
このとき、四角形EFGHの面積はア㎠です。
【ヒント】
いろいろな解き方があると思います。今回はおまけの解答含めて2つご紹介します。
すぐに思いついた方法は、3:4:5の直角三角形に注目し、下図のような補助線をいれ、
分割して面積を出す方法です。
台形ABCDの面積はすぐにわかりますし、求める面積以外の三角形の面積もわかりそうです。
【解答】
台形ABCDの面積は(2+5)×4×\(\displaystyle\frac{1}{2}\)=14㎠
三角形FBIは3:4:5の直角三角形となりますので、
FI=4×\(\displaystyle\frac{2}{5}\)=\(\displaystyle\frac{8}{5}\) ,BI=3×\(\displaystyle\frac{2}{5}\)=\(\displaystyle\frac{6}{5}\)
三角形FBC=5×\(\displaystyle\frac{8}{5}\)×\(\displaystyle\frac{1}{2}\)=4
三角形FCG=1×(5-\(\displaystyle\frac{6}{5}\))×\(\displaystyle\frac{1}{2}\)=\(\displaystyle\frac{19}{5}\)×\(\displaystyle\frac{1}{2}\)=\(\displaystyle\frac{19}{10}\)=1.9
三角形AEKも3:4:5の直角三角形となりますので、
AK=4×\(\displaystyle\frac{1}{5}\)=\(\displaystyle\frac{4}{5}\) ,EK=3×\(\displaystyle\frac{1}{5}\)=\(\displaystyle\frac{3}{5}\)
三角形EAD=2×\(\displaystyle\frac{4}{5}\)×\(\displaystyle\frac{1}{2}\)=0.8
三角形EDH=2×(\(\displaystyle\frac{3}{5}\)+2)×\(\displaystyle\frac{1}{2}\)=\(\displaystyle\frac{13}{5}\)=2.6
となります。求める青い部分の面積
四角形EFGH=台形ABCDー(△FBC+△FCG+△EAD+△EDH)
=14-(4+1.9+0.8+2.6)=14-9.3=4.7㎠・・・(答え)
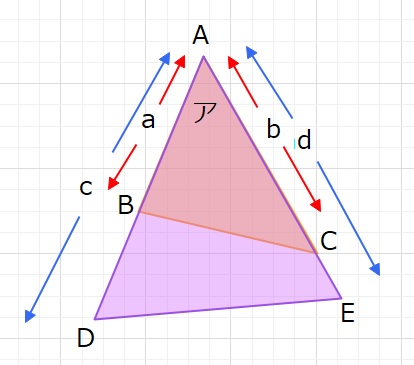
【おまけ】角度の大きさが ア で同じ三角形ABCと三角形ADEがあるとき、
面積比 は a×b : c×d となることを知っている人は、これを活用しても解けます。
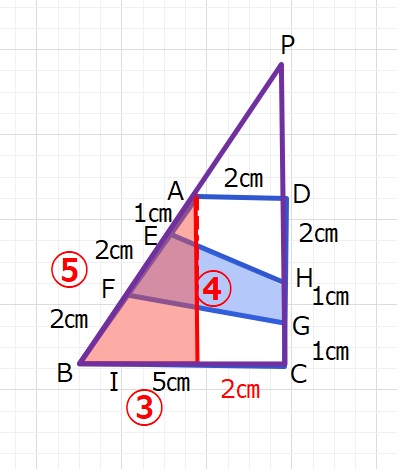
下図のようにAB,DCの直線を延長して点Pを作ります。
三角形PADは3:4:5の直角三角形となりますので、
PD=2×\(\displaystyle\frac{4}{3}\)=\(\displaystyle\frac{8}{3}\),PA=2×\(\displaystyle\frac{5}{3}\)=\(\displaystyle\frac{10}{3}\)
PH=\(\displaystyle\frac{8}{3}\)+2=\(\displaystyle\frac{14}{3}\),PE=\(\displaystyle\frac{10}{3}\)+1=\(\displaystyle\frac{13}{3}\)
PG=\(\displaystyle\frac{8}{3}\)+3=\(\displaystyle\frac{17}{3}\),PF=\(\displaystyle\frac{10}{3}\)+3=\(\displaystyle\frac{19}{3}\)となります。
△PAD:△PEH:△PFG=PA×PD:PE×PH:PF×PG
=\(\displaystyle\frac{10}{3}\)×\(\displaystyle\frac{8}{3}\):\(\displaystyle\frac{13}{3}\)×\(\displaystyle\frac{14}{3}\):\(\displaystyle\frac{19}{3}\)×\(\displaystyle\frac{17}{3}\)
=10×8:13×14:19×17=80:182:323 となります。
よって△PAD:四角形EFGH=80:323-182=80:141
今△PADの面積は2×\(\displaystyle\frac{8}{3}\)×\(\displaystyle\frac{1}{2}\)=\(\displaystyle\frac{8}{3}\)なので、
四角形EFGH=141×\(\displaystyle\frac{8}{3}\)×\(\displaystyle\frac{1}{80}\)=\(\displaystyle\frac{141}{30}\)=4.7㎠・・・(答え)となります。


コメント