2023年 灘中入試問題より
【問題】
まっすぐな道路に地点Pと地点Qがあります。Aさんは地点Pを出発して地点Qに向かって歩き,地点Qに着くとすぐに折り返して地点Pに向かって歩きます。Aさんが地点Pを出発するのと同時にBさんは地点Qを出発して地点Pに向かって歩き始め,地点Pに着くとすぐに折り返して地点Qに向かって歩きます。AさんもBさんも,それぞれ常に一定の速さで歩きます。Aさんが地点Pを出発してx分後のAさんとBさんの距離をymとします。Aさんが地点Pを出発したのち再び地点Pに着くまでの間のxとyの関係は次のグラフのようになりました。このとき,地点Pと地点Qの距離は[①]mです。また, Aさんが地点Pを出発して[②]分後に,AさんとBさんは初めてすれ違います。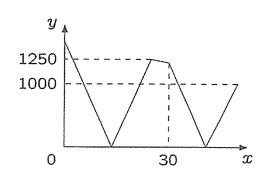
【ヒント】
30秒の直前のグラフよりAの方がBより早いことがわかります。
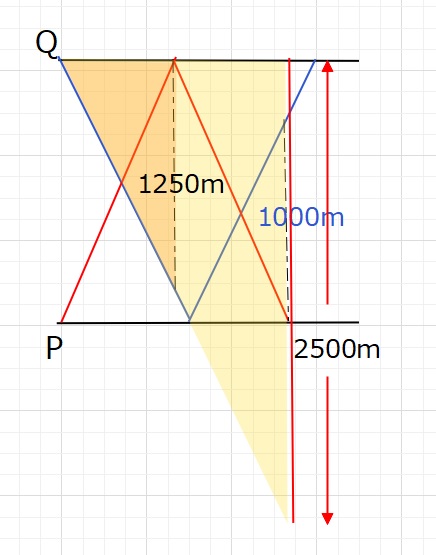
Aを赤線で、Bを青線でダイアグラムに書きなおし、相似を活用して解きます。
状況を把握するまで、戸惑いますが、情報が整理できれば簡単にとけます。
【解答】
①AがQに初めて到着したとき、Bは1250m進んでいます。
Aが折り返し、Pに到着したとき、Bは2500m進みます。
よって、PQの距離は 2500-1000=1500m・・・(答え)
②Bの速さは、1500÷30=50 m/分とわかります。
よってAとBの速さは、1500:1250=6:5ですので、
Aの速さは 6:5=A:50より 60 m/分です。
最初に出会うのは 1500÷(60+50)=\(\displaystyle\frac{150}{11}\)
=13\(\displaystyle\frac{7}{11}\) 分後 ・・・(答え)


コメント