2023年 灘中入試問題より
【問題】
ある国で使われる通貨の単位は「ナダ」です。円・ナダ取引において,円に対するナダの値段は毎日1回変化し,前日より安くなるか高くなるかのどちらかです。ある日1ナダは150円でした。Aさんはその次の日から以下のような方法で円・ナダ取引を始めました。前日よりナダが安くなれば持っている円の半分をナダに替え,前日よりナダが高くなれば持っているナダの半分を円に替えます。Aさんは最初5760円のみを持っており,ナダは持っていませんでした。1ナダは取引1日目は120円でした。前日よりナダが安くなったので,1日目の取引の後Aさんの所持金は2880円と24ナダになりました。1ナダは取引2日目は90円,取引4日目は180円で, 4日目の取引の後Aさんの所持金のうち円は5940円でした。このとき,取引3日目の1ナダは最も高い場合で[①]円,最も安い場合で[②]円です。ただし,Aさんがしたすべての取引について,1円未満,1ナダ未満の端数は生じませんでした。また,手数料などは考えないものとします。
【ヒント】まずは2日目のナダを計算して、ルールになれます。
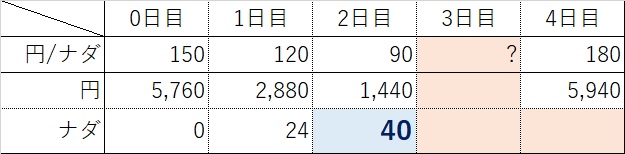
2日目は90円/ナダと下がったために、2880円の半分、1440円をナダにかえます。
1440÷90=16ナダとなり、24+16=40ナダです。
3日、4日目は前日に比べ、1.(下、下)2.(下、上)3.(上、上)4.(上、下)の4パターンが
ありますが、4日目が180ナダなので(下、下)はありえません。
よって2、3、4の3パターンを考えます。
【解答】それぞれ、2、3、4の場合に表のなかの①②③④の順に丁寧に計算します。
短時間で処理すると、頭が混乱します。(笑)表の中の計算式は正確に表現できてません
が、注釈で補足します。
最も高い 522円 最も安い 40円・・・(答え)
2.(下,上)の場合

①1440÷2=720円分をナダに変えます。
②4日目は5940円持っているので、5940-720=5220円分、ナダを円に替えました。
つまり4日目は5220÷180=29ナダ分替えました。
③3日目のナダは4日目のナダから類推して29×2=58ナダです。
④3日目の1ナダ当たりのレートは58-40=18ナダ交換して720円なので、
720÷18=40円/ナダ です。
3.(上,上)の場合

①1ナダあたりのレートが上がりますので、もってるナダの半分の20ナダを替えます。
残りは40-20=20ナダ
②4日目もあがりますので、持ってるナダの半分10ナダを替えます。(残り10ナダ)
③4日目にレート180円で10ナダかえたので、1800円増えてます。
よって、3日目の円は5940-1800=4140円です。
④2日目と比べ3日目は4140-1440=2700円増えてます。
20ナダ交換したので、交換レートは2700÷20=135円/ナダとなります。
4.(上,下)の場合

①1ナダあたりのレートが上がりますので、もってるナダの半分の20ナダを替えます。
残りは40-20=20ナダ
②4日目は3日目よりも交換レートが下がるので、3日目の半分を円からナダに替えています。
つまり3日目は5940×2=11880円持っていました。
③11880-1440=10440円で20ナダ交換したので10440÷20=522円/ナダです。


コメント