今日は、九去法(きゅうきょほう)と呼ばれる確かめ算の方法をご紹介します。
九去法を知るまえに、これは算数の範囲ではないのですが、合同式とよばれる
便利な考え方をご紹介します。
17と26という2ケタの2つの数字があるとします。
この数字を9で割った余りについて考えてみましょう。
17は9×1+8で、26は9×2+8となりますので、
17と26それぞれを9で割った余りは、同じ8となります。
この余りが同じ数字を、
17≡26(mod9) と書くことにします。
17 ごうどう 26 モッド9と読み、これを合同式といいます。
同様に 10と19という数字は、9で割った余りがそれぞれ1で等しいですので、
10≡19(mod9)と書くことができます。
ここで、 左どうしと右どうしをたした、27(17+10)と45(26+19)に
ついて考えてみましょう。
この2つの数字も、9で割ると、余りが0で等しくなりますので、
27≡45(mod9) つまり、≡ の左辺どうし、右辺どうしは自由に
たしてよいとわかります。(正式にはもう少し詳しく証明しなければいけませんが)
同様に、差(ひき算)も成り立ちます。
さらに、かけ算も成り立ち、わり算については条件付きで成り立つことがわかります。
わり算については今回は詳しくは触れません。
ウラ技1
上で説明したとおり、 ア≡イ(mod ウ)が成り立つ場合、
1.アーイ≡イーイ≡0(mod ウ)
2.ア+イ≡イ+イ(mod ウ)
3.ア×イ≡イ×イ(mod ウ)
と普通の式の計算でできることがそのままできます。
≡は=同様に何個でもつなぐことができます。
この性質を使うと、考え方の幅が広がり、とても便利です。
九去法について たし算・ひき算編
最初に、九九(クク)の九の段について、じっくり見ています。
9×1=09
9×2=18
9×3=27
9×4=36
9×5=45
9×6=54
9×7=63
9×8=72
9×9=81
あえて9を09と書きましたが、なにか気づきましたでしょうか!
そうです、1ケタ目の数字が、9,8,7,6・・・1となっていて、
2ケタ目の数字が0,1,2・・・8ときれいに並んでいます。
さらに、1ケタ目と2ケタ目の数字の合計が0+9=9,1+8=9,2+7=9
とすべて9になるのです。
このことからも想像できるように
①9の倍数の見分け方は、「各ケタの数字の和が9の倍数である」かです。
また、321という数字は、100の位が3、10の位が2、1の位が1なので
3×100+2×10+1×1と表現できます。
ちなみに 1も10も100も9で割った余りが1となりますので、
②1≡10≡100≡1000・・・・・(mod9) と表現できます。
この①と②の性質が九去法のタネとなります。
【数字根の作り方】 例)24653
数字根は占いなどで見たことがあるかたもいるかもですが、
各桁の数字をたしていき、1ケタの数字になるまでたした数字のことです。
上の例では「2」+「4」+「6」+「5」+「3」=20 ・・・①
さらに、「2」+「0」=2と計算します。 ・・・②
1ケタの数字になったのでここで終了です。
下のように合計が9になるように一気に消す方法もあります。
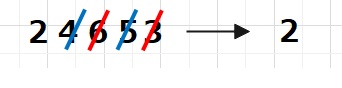
以上を活用し、検算するのが 九去法です。それでは実際にやってみます。
【例】1999+2022=4021 が正しいかどうかの確かめ算について考えます。
ここで、9去法とよばれる方法を紹介いたします。9去法は名前のとおり、9を
とりさっていくという方法です。
1999の数字の9を取り除くと、1000となり、
各桁をたすと1+0+0+0=1となります。
また2022は9がなくまた、2+0+2+2を計算すると6となります。
さらに1+6=7を計算します。
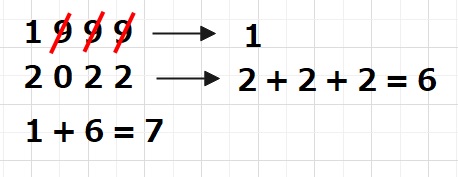
今回は9がこれ以上いけないので7となりますが、
たとえば12となった場合は、1+2=3とさらに各桁をたします。
さて、計算結果の4021について、9がないので、そのままたすと
4+0+2+1=7となり、先ほどの左で計算した結果と同じ7となりますので
計算がただしいことがわかります。
このように、左と右を別々に検算し、同じ数字になれば正しいと判定できます。
これは実は100%間違いを発見できる方法ではないのですが、実際のなかでは
ほぼ100%に近い効果があります。
是非使ってみてください。
九去法 かけ算編
【例】6799×9279=63087921 が正しいかについて考えてみます。
たし算・ひき算同様に、
6799から9を除くと6700となり6+7+0+0=13、1+3=4となります。
9279から9を除くと0270となり0+2+7+0=9≡0となります。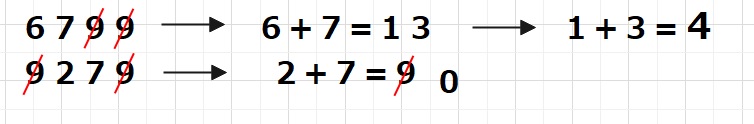
よって左辺は4×0=0となります。
また、63087921
→63087021
→6+3+0+8+7+2+1→27
→2+7=9→0となり、
左辺と右辺が一致するので会ってることがわかります。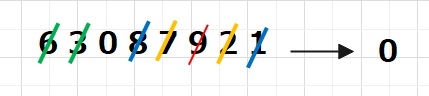
慣れるまですこし、混乱するかもですが、なれると5秒程度でたしかめ算ができますので
是非チャレンジして自分のものにしてください。

コメント