【問題】すべて分母が2026の、2026分の1から2026分の2026までの分数で、既約分数(分子と分母が互いに素)の和はいくらか。互いに素とは、共通の約数が1しかない2つの数のことです。
【ヒント】たとえば分母が「10」のとき
この中で約分できないのは?
約分できない分数は、たすと 1 になるペアが作れます!
【解答】
例えば、
を足すと、
同じように、
というように、分子が「たして 2026 になるもの」は、必ず 1 になります。
2026は
1013は素数です!
このとき、
数字「あ」が 2026 と互いに素なら
2026−「あ」 も必ず互いに素
既約分数は、必ず「1になるペア」を作る
「2026と互いに素な数」はいくつあるか考えます。
1〜2026の中で、2の倍数と1013の倍数を除くと、ちょうど 1012個あります。
既約分数は 1012個、2つで1になるペアなので、
それぞれのペアの和は 1なので、、
答え、506 となります。
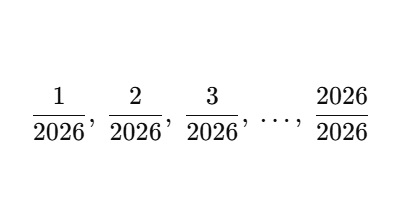

コメント