【問題】
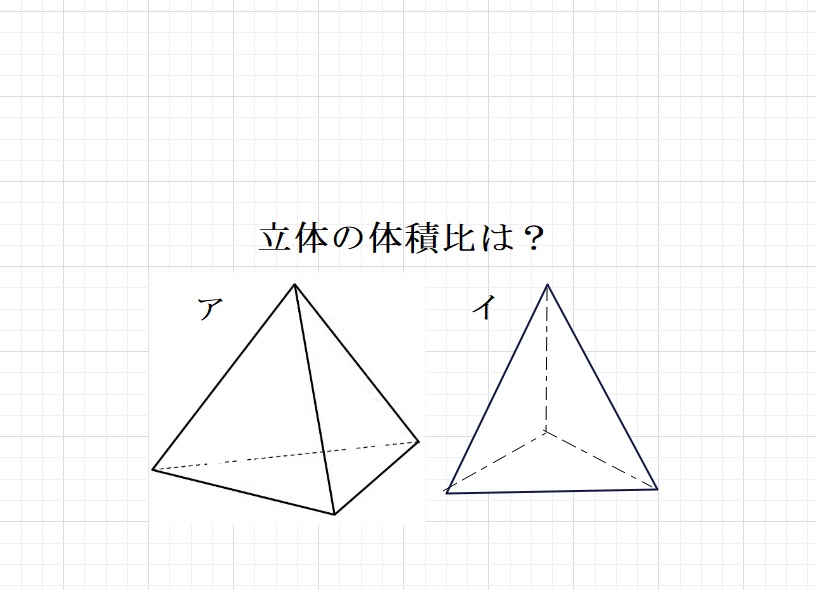
図のような、立体ア、イがあります。アの4つの面はすべて合同な正三角形です。
アの面の1つはアの面と合同な正三角形で、残りの3面はたがいに合同な直角二等辺三角形
です。この種類の三角すいを何個か使ってできる立方体のなかで最もちいさいものの
体積は60㎤でした。このとき、三角すいアとイの体積はそれぞれいくつでしょうか。
【ヒント】
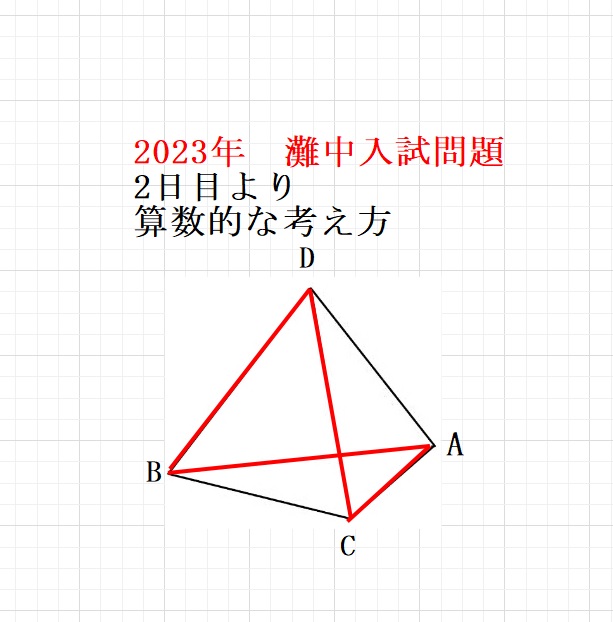
以前ご紹介した図をつかいます。
こちらもご参照ください。★★★☆☆中級コース 正四面体の面積 | 算数コロシアム (mathcolo.com)
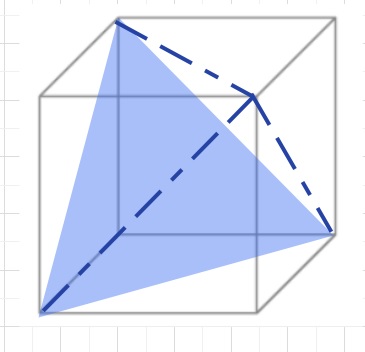
三角すいア1個と、その周りに三角すいイ4個
を組み合わせると、図のような立方体ができます。また、
その際、三角すいイの体積は立方体の体積の 1×1×\(\displaystyle\frac{1}{2}\)×\(\displaystyle\frac{1}{3}\)=\(\displaystyle\frac{1}{6}\)
です。よってア=1-\(\displaystyle\frac{1}{6}\)×4=\(\displaystyle\frac{2}{6}\) =\(\displaystyle\frac{1}{3}\) です。
【解答】アの体積は 60×\(\displaystyle\frac{1}{3}\)=20㎠・・・(答え)
イの体積は 60×\(\displaystyle\frac{1}{6}\) =10㎠・・・(答え)
コメント