2021年 甲陽学院中学入試問題より
【問題】
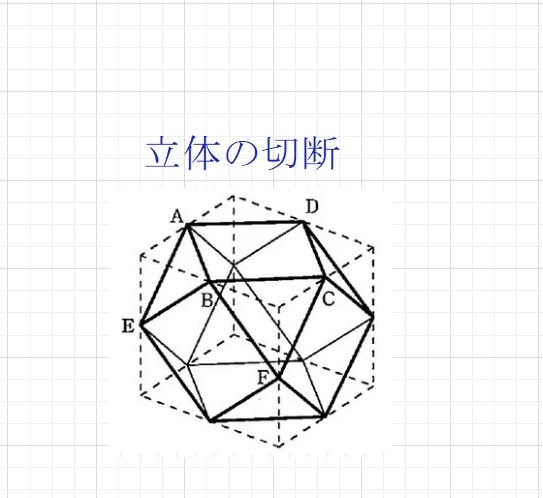
図のような立体の各辺の真ん中の点を結んでできた立体X
があります。
(1)辺BEの真ん中の点Mをとおり、面ABCDに平行な平面で
立体Xを切断するとき、立体Xの断面積は面ABCDの面積の何倍ですか。
(2)BN:NE=1:2となるように、辺BE上に点Nをとります。
点Nを通り、面BCFに平行な平面で立体Xを切断するとき、
立体Xの断面積は面BCFの面積の何倍ですか。
【ヒント】
(1)断面図とそれを上からみた図は下のようになります。
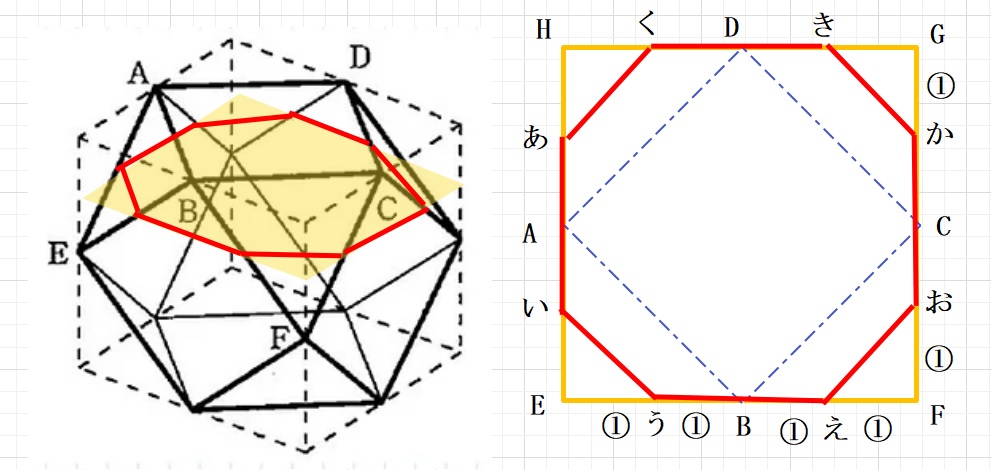
(2)(1)で慣れたところで同様に断面図と上からみた図を書いてみます。
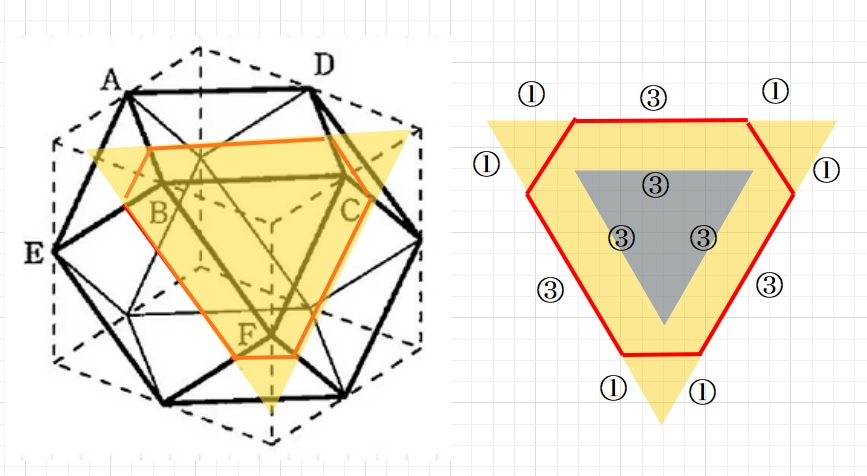
【解答】
(1)今正方形EFGHの1辺を4とすると、正方形ABCDは4×4×\(\displaystyle\frac{1}{2}\)=8
「8角形あいうえおかき」は 4×4-1×1×\(\displaystyle\frac{1}{2}\)×4=16-2=14
よって14÷8=\(\displaystyle\frac{7}{4}\)=1\(\displaystyle\frac{3}{4}\)倍・(答え)
(2)BCFの面積を⑨(3×3)とすると、黄色い正三角形は㉕(5×5)となります。
3つの角のスミはそれぞれ①ですので赤い6角形は㉕-③=㉒
よって\(\displaystyle\frac{22}{9}\)=2\(\displaystyle\frac{4}{9}\)倍・・(答え)
コメント