n進数(エヌシンスウ)とは
n進数とは、n種類の記号を用いて数を表現する方法をn進法といい、またn進法で表された数をn進数という。
例えば、私たちが日ごろ使っている10進法は、0,1,2,3,4,5,6,7,8,9という10種類の記号を用いて数を表現しています。
2進法といえば、0,1の2種類の記号を用いて普通は表現します。
それでは10種類以上の記号が必要な16進法はどうでしょうか?
10種類に加えA,B,C,D,E,Fの6種類の記号を用いて数を表現します。
n進法ではn個集まると桁(ケタ)がくり上がります。
・たとえば10進法では9の次は、10となります。
・2進法では1の次は10です。
・16進法では、Fの次は10です。
n進法を式で表すと?n進数を10進数で表す
・10進法で24653は式で表すと、2×\(10^{4}\)+4×\(10^{3}\)+6×\(10^{2}\)+5×\(10^{1}\)+3×\(10^{0}\)となります。
・2進法で10001は10進数で表すと、1×\(2^{4}\)+0×\(2^{3}\)+0×\(2^{2}\)+0×\(2^{1}\)+1×\(2^{0}\)となります。
・ここで10001は何進数の数なのかが区別がつきません。そのため、例えば2進数の場合は、
10001\(_{(2)}\)のように表記して区別します。何も表記がない場合は普通は10進数表記です。
10進数をn進数で表す
2023という数字を考えてみます。
これを16進数で考えると、16単位でケタがくり上がるので、下のように16でわっていきます。
まず、2023を16で割ると、126余り7となります。さらに126を16で割ると7余り14となります。
さらに7を16でわると0あまり7となり、これ以上は割れそうもありません。
ここで終了で余りを下から順に表記すると 7 14 7 ですが、14は16進数ではEですので
2023は 7E7\(_{(16)}\) となります。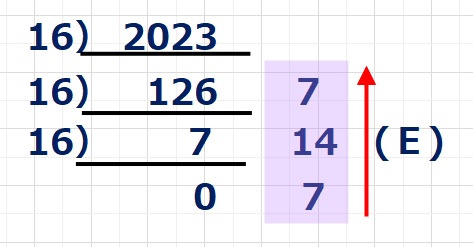
n進数からn進数への変換
これは、上をく合わせて、n進数を一度10進数へ変換し、それをさらに求めるn進数変換するという作業を実施します。



コメント