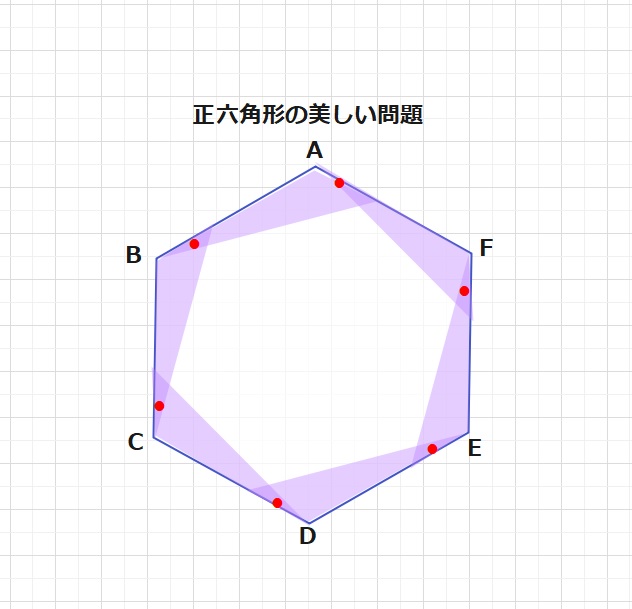
【問題】図の●の角の大きさが6個すべて15°であるとき、それを1つの角とする
紫の三角形6個を取り除いてできる白い正六角形の面積は、
もとの正六角形ABCDEFの面積の面積の何倍ですか。
【ヒント】
点DをとおりADに直角になるようにGDをとりますと、∠HDG=30°となります。
∠LCD=∠BCD-∠BCL=120-15=105°なので、
∠GCD=75°となります。 よって∠CGD=75°となり、△DCGはDC=DGの
二等辺三角形であることがわかります。
CDは正六角形の一辺なので、CD=DG=DEとなり、三角形DEGもDE=DGの二等辺三角形
となります。
また、CEとDGは平行ですので、
△CGDと△EGDの面積は等しくなり、△CGHと△EDHの面積も等しくなります。
つまり、四角形LCHKと△EHDの合計は正三角形GKLと等しくなります。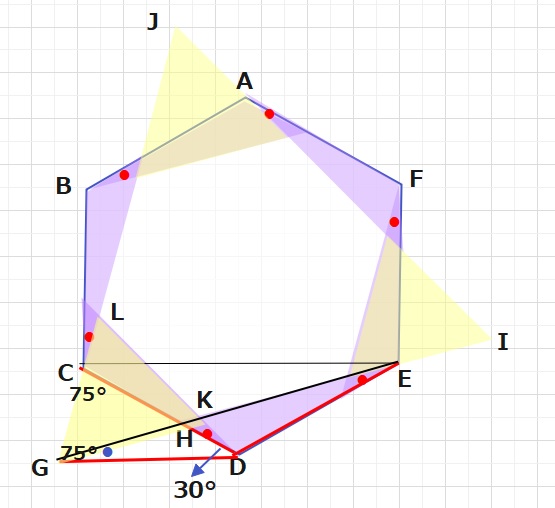
【解答】
上の図より紫の部分の面積の合計は黄色の正三角形3つと等しくなります。
また白い正六角形は、黄色い正三角形6個分です。
よって正六角形ABCDEFは黄色い正三角形9個分となります。
白い正六角形は正六角形ABCDEFの\(\displaystyle\frac{6}{9}\)
つまり\(\displaystyle\frac{2}{3}\)倍・・(答え)
コメント